Boxing is a fighting sport where the goal is to harm your opponent to achieve a higher score. Boxers have to condition their body on a regular basis to increase their fighting skills in speed, power and technique. If you have watched any professional boxing match, you would know how intense the fights can get. In most matches, the boxers’ faces would have taken so much damage they start bleeding.
Given this situation, the way to win is to land as much punches to their opponent’s face and body. However, if the opponent knows this, he will choose to avoid damage and try to deal damage of his own. In the boxing ring, a boxer can do one of the four actions: attack, defend, maneuver or observe. These choices apply Game Theory and is an instance of the Zero Sum situation.
When a boxer attacks, he can be nullified by a block. The attacker will lose some energy while the blocker sustain much lesser to no damage. Attacks can also be negated by a maneuver, making the attacker waste energy, balance and sight.
When a boxer defends, he will prepare for an attack but would reduce his sight.
When a boxer observes, he is looking for a perfect opportunity to attack, increasing his accuracy and critical hit chance.
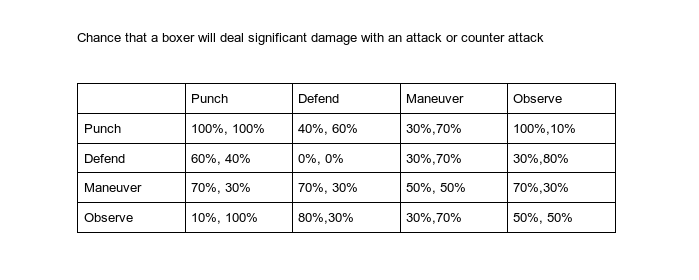

Interesting – this seems like a slightly augmented take on the classic rock-paper-scissors game. However, there’s a concept of a delayed payoff here, which is that you basically ‘skip’ a turn and hope that down the line there’s a better opening.
I wonder how we can represent this as payoffs in a game? What if for each payoff it was actually a function and each payoff evaluation was the input to the function? I’m just spitballing here – I’m not sure if that even makes sense haha.
Good take though – but maybe you could back this up with some sources and data?