Google map is the most popular mapping service in the world. Its two main features are real-time traffic conditions and route planning for traveling by foot, car, bicycle and air, or public transit. My topic is that how Google map ultilizes the graph theory to navigate users to their destinations.
In the context of CSCC46, a map can be represented as a weighted and undirected network or graph. It has nodes and edges. Similarly, Google Map can be viewed as such with nodes as locations and edges as roads. Oftentimes, people want to get to some places as fast as possible. Therefore, the Dijkstra’s algorithm comes in handy when calculating the shortest path between places. When the algorithm does is that, given a weighted graph, a starting point and an endpoint within the graph itself, the algorithm finds a path at minimum weight. In the case of Google map, it finds the fastest route from one point to the other as the pictures shown below.
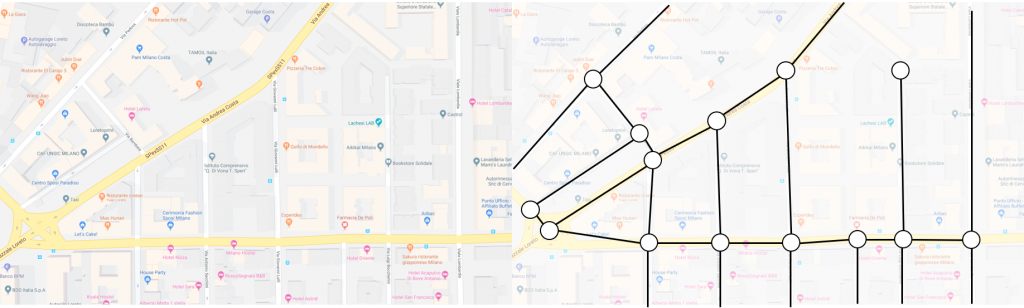
Of course, each edge has different weight. Not only does the map take distances beween nodes into account, but also it considers the traffic volume of the road. As the pictures shown below, the red segments indicates that the traffic volume is high and the green ones mean the road is clear. Because sometimes, a fastest path does not mean a shortest path. By considering the traffic volume as another weight of edge, Google map calculates fastest paths as accurate as possible.
This example demonstrates that the pratice of information network plays an important role in our daily life. By studying it, we can have a deeper understanding how the individual entity interacts with others and how they are grouped together to become a network so that it can be an important reference when a new technology is being developed.

Reference: https://magazine.impactscool.com/en/speciali/google-maps-e-la-teoria-dei-grafi/
