Game Theory is dependent on the idea of Nash equilibrium. Nash equilibrium, the situation when neither of the players can choose any other strategy than the one in Nash equilibrium in order to get a better payoff. We can apply the same in the sport of basketball. Imagine a game coming to a winning shot. There are certain scenarios in order to win the game and to lose the game. Considering one of the situations where the loosing team is down by two points, has ball possession and say 20 seconds on the shot clock and the game as well. The team takes a shot. The shot can be either a two-pointer or a three-pointer, two-pointer having higher possibility. With a two-pointer the game would go into an overtime, but instead having a three-point shot, although with less probability, would help win them the game. The paper assumes having a 50% chances of winning upon going into overtime. On the other hand, the current winning team also has two choices. One is to defend the three-pointer, while risking an open two-point shot. The other is to defend the two-pointer shot, but risk the three-pointer shot from the opposite team.
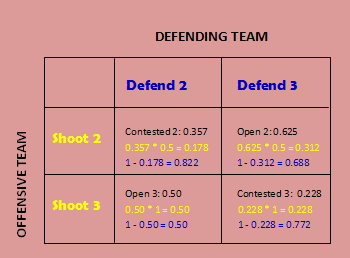
Based on the data collected in the paper, there is no dominant strategy for either team. They have to play a mixed strategy in order to be unpredictable for the other side. After some calculations, the mixed strategy equilibrium comes out to be (p , q) = (0.670 , 0.207), p being the chances of offensive team taking two-point shot and q being the chances of defending team saving the two-point. For the leading team to win, they should defend the three-point shot and not worry about the overtime as in that they would have a 50% chance to win as previously seen. The decision is a tough one for both sides and this relates to many real life interesting situations such as this Finals game.
Reference:

This is an interesting situation to apply game theory, and it is hard for both offense and defense team to judge on fly what to do in the last few seconds of a tournament. Other then consider a general winning probability of a team, we can also consider which player is holding the ball at the moment. Depends on different players, we will have more cases to consider and the strategies might be different. It will be more interesting to see what is the payoff for both teams under that calculation.
Very well done explanation with numbers. Wouldn’t real life situations be a bit more complex since if the losing team was forced to score too early, then the winning team can score again.
No, if there’s 20 seconds on the clock, the only way to force an early shot is if the ball is going to be turned over. Although I do believe this model oversimplies the analytics by a fair bit because getting an open look from the midrange is far easier than from 3. That is to say, the offense wouldn’t look for specifically a 2 pointer or 3 pointer to force OT (since they are already in a losing position), but they would take whatever open look they get.
Interesting! I have a friend who works for an NBA team as a statistics analyst and part of his job is to analyze shooting percentages and behaviors of players so as to maximize points per his team’s player shot, and lower points per shot for opposing teams. It would be interesting to see if they call it game theory or some other term.