We have seen power law applications arise naturally in many applications with networks, and it also appears in a sport heavily studied by statisticians: baseball. Researchers at Boston University found that the length of player careers in Major League Baseball (both pitchers and batters) followed a power law distribution (Petersen, Woo-Sung, & Eugene, 2008). The study recorded all players with careers ending between the years 1920 and 2000.
Baseball like many other professional sports, is incredibly competitive. What makes baseball unique to other team sports is that there is a team dynamic, but there are many individual battles between pitchers and batter which can determine the outcome of a game. In the study measured to determine typical major league career longevity, both pitchers and batters were found to have similar projected career longevity. I found this surprising, considering how we hear of pitchers facing serious, sometimes career-ending arm injuries. Career longevity was measured using a similar metric for both pitchers and batters, with pitcher longevity measured in number of innings pitched, and batter longevity in number of at-bats.
In terms of power law distribution, the “heavy-tail” part of the distribution was for players with extremely short careers of only a few games, for both pitchers and batters. By contrast, there were very few players who maintain long careers. The longevity of all these players careers were affected by similar factors.
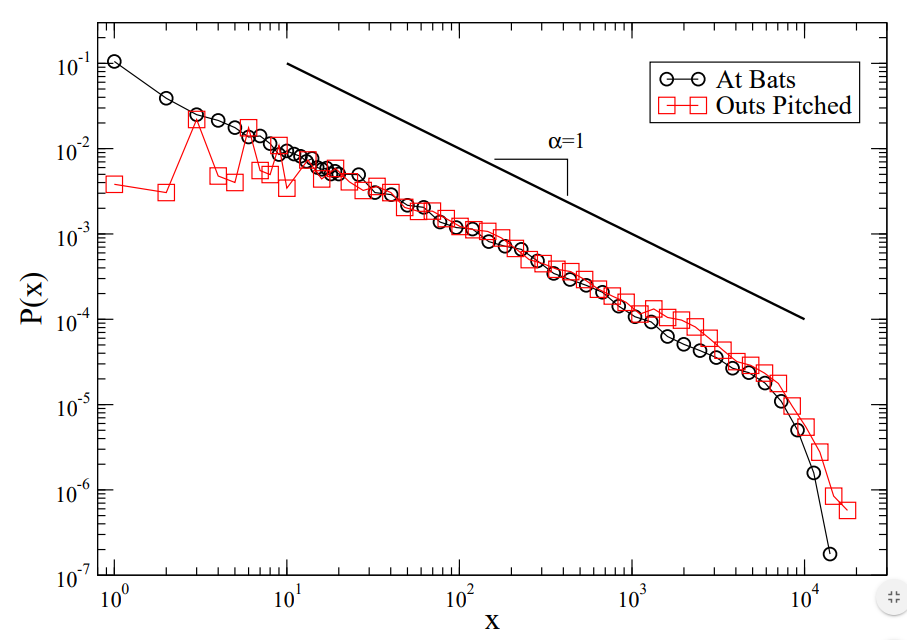
The greatest factors were suspected to be the league’s relatively long regular season compared to other sports (162 games), and the competitiveness of the league. Due to the long regular seasons, players often play games with limited rest, and require occasional substitution with less skilled players for some games. In addition, temporary injuries to regular players during the season allow for new players to break out of the minors and enter the league as a temporary replacement. However, many of these new players do not maintain long careers as they are not sufficiently skilled to remain in the league, accounting for many players having very short (a handful of games) careers.
The greatest factors were suspected to be the league’s relatively long regular season compared to other sports (162 games), and the competitiveness of the league. Due to the long regular seasons, players often play games with limited rest, and require occasional substitution with less skilled players for some games. In addition, temporary injuries to regular players during the season allow for new players to break out of the minors and enter the league as a temporary replacement. However, many of these new players do not maintain long careers as they are not sufficiently skilled to remain in the league, accounting for many players having very short (a handful of games) careers.
The same injuries to players also affect player longevity, where some injuries can be career-ending, others cause small reductions in performance. Since the league’s competitiveness level remains consistent, as players age, and/or develop more injuries, they may no longer be competitive enough to remain in the league. Highly skilled players who were initially more competitive, with many injuries over a long career, maintain long careers since their reduction in performance due to accumulated injuries or age drops them closer to “average” level over time. Less skilled players seeing a minor drop in performance may already be close to “average” and risk being cut from the team. Despite the specializations of pitchers and batters and different injury types, their career longevity was similar.
This relates to what we have learned in CSCC46 because it is a real-world example of a heavy-tailed distribution of data which arises naturally without having this sort of pattern emerge as an intended goal. It shows an example of where power laws emerge naturally. This power-law distribution also remained consistent through major league baseball for decades, surviving many changes in MLB which could have affected career longevity, such as various expansions of the league (diluting skill among teams), the steroid era boosting home run counts, and the rise of the radar gun favouring harder-throwing pitchers, (who may have increased potential for injury).
This study shows the persistence of this power-law distribution even when the development of this distribution was unintentional. It shows that when conditions favour the emergence of these sorts of patterns, that even decades of different changes in MLB do appear in the data, but do not make any significant changes on the distribution of player longevity.
Source: Petersen, A., Woo-Sung, J., & Eugene, S. H. (2008, September). On the distribution of career longevity and the evolution of home run prowess in professional baseball. EPL Europhysics Letters, 83, 50010. doi:10.1209/0295-5075/83/50010