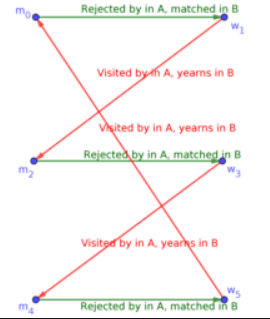
In an article made available on-line the 13th of September 2019, titled “Incentives and implementation in marriage markets with externalities,” academics María Haydée Fonseca-Mairena and Matteo Triossi discuss the use of Nash Equilibrium to implement stable correspondences in marriage markets with externalities. As in CSCB36H3, the term “marriage market” refers to markets consisting of two non-empty, distinct, and mutually exclusive sets which need to paired off. Examples include: marriages, dance partners, and medical students and medical schools.
A quick review of CSCB36 material: in marriage market algorithms we assume that all parties are acting rationally, and that rational actions must include preferring any pairing over being on your own. Stable matches are matches that are not blocked by a pair. That is, no pair of participants in the market should prefer to be matched together over their assigned match. In CSCB36 we proved that in marriage markets without externalities, the dominant strategy is to be honest about your preferences and to reach out to members of the other group.
Without externalities, honesty and initiative will secure an optimal match. In their article Fonseca-Mairena and Triossi examine the best strategy in marriage markets with externalities.
We all know that some of the algorithms and examples covered in many of our classes work only for simple or specific requirements that do not often occur organically in the real world. Often, in life, marriage markets include externalities – that is, the pairings effect more people than just the two members who have been matched. Consider the examples above; family members and friends likely care about who your spouse is, in dance competitions each pair is interested in who their competitor’s partner is, medical students are likely concerned not only with the school they are accepted to themselves, but also the school that accepts their friends and classmates. When taking externalities into account the concept of a stable matching changes. In marriage markets with externalities, a stable matching M is blocked by an individual if they prefer being alone to the pair they are assigned to in M. A stable matching can also be blocked by a pair if they prefer any matching in which they are paired together over their assigned matches in M.
Fonseca-Mairena and Triossi prove out that in a marriage market with externalities the honest and initiative-taking dominant strategy applied to marriage markets without externalities no longer works. In their article, Fonseca-Mairena and Triossi further prove that Nash equilibrium can be used to implement stable matches in marriage markets with externalities. As a CSCC46 student, I found this article interesting due to its potential applications. As mentioned above, in class we often learn about algorithms or theories that appear to have limited applications in the real world. With our lectures on game theory especially the examples seemed over-simplified and specific. I felt that it was unlikely you would come across such simple examples in real like where there are often many factors to consider. I understand, of course, that the examples were simplistic because the lectures were only introducing us the game theory, and simple examples made our professor’s points more clear. However, the use of Nash equilibrium to create stable matches in marriage markets with externalities suggests countless real world applications. There are the three examples in the introduction to this blog, but also countless others. Many people, from parents, teachers, managers, to administrators of various levels find themselves attempting to create a set of stable pairings for an activity or event. Fonseca-Mairena and Triossi ‘s article provides proof of a simple method for choosing.
RESOURCES:
[1] Fonseca-Mairena, M. H., & Triossi, M. (2019). Incentives and implementation in marriage markets with externalities. Economics Letters, 185 doi:10.1016/j.econlet.2019.108688
[2] Stable marriage problem. In Wikipedia. Retrieved November 15, 2019, from https://en.wikipedia.org/wiki/Stable_marriage_problem .
[3] How the internet has changed dating. In The Economist. Retrieved November 15, 2019, from https://www.economist.com/briefing/2018/08/18/how-the-internet-has-changed-dating .