Author: Sherry Hoi Yan Ma

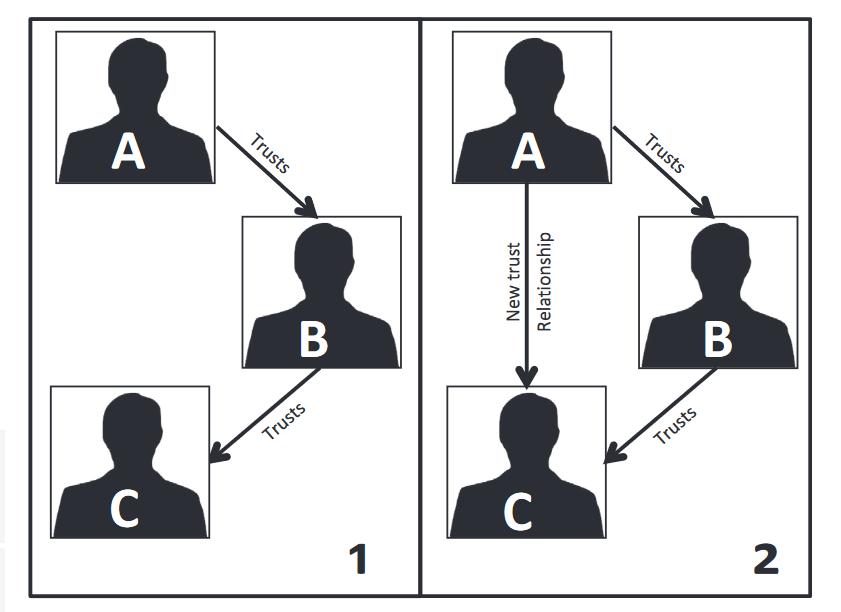
In today’s modern day, people are connected with other people; not just in school or at the workplace, but also on the Internet. There are various popular social applications such as Facebook, Twitter, and Instagram which allow us to get in touch with our friends. With the introduction of online dating in social networks, people are able to find romantic partners online in ways never imaginable before. However, the communication will be most likely happen on the Internet, which gives people the option to meet up in real life only if they are comfortable in doing so.

This topic is relevant to the study of Game Theory, which we covered in class with some examples about how two people (or groups) will select a strategy that provides the highest payoff or benefits. Most people, if they are rational, will choose the best strategy based on what other people choose (i.e. dominant strategy). In the perspective of dating app users, the following example below illustrates the mindset of when they engage in a conversation with another user, which relates very closely to the Prisoner’s dilemma that was also covered in class.

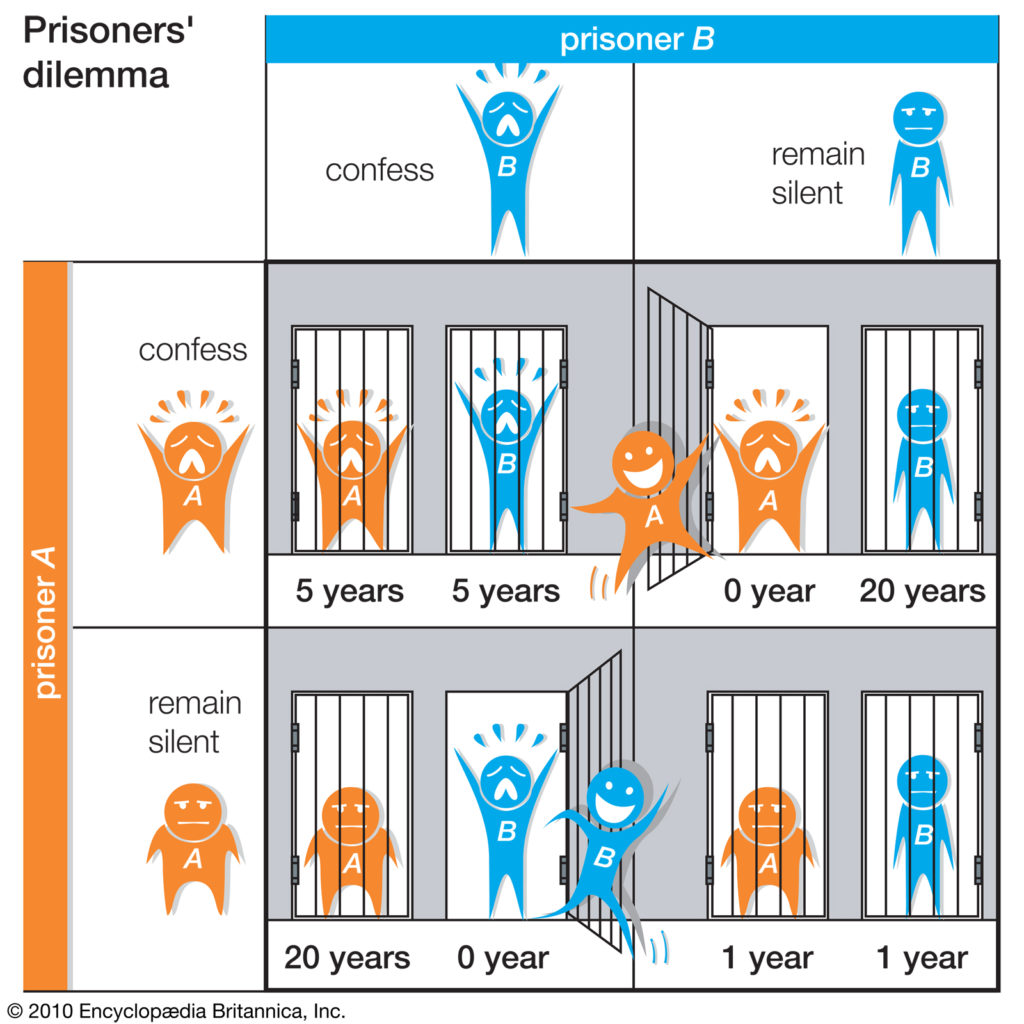
Alice and Bob are users on a dating application and they found each other on the application, wanting to know more about each other. Bob initiates the conversation and they both have a good time talking. Later on, they decide to go on a date, and it goes great. They both feel good about each other and they now like each other, but none of them have asked the other to confirm their current status. Moreover, they did not text each other after the date. After two days from the date, Bob finally decided to ask Alice if she wanted to hang out with him. He did not contact Alice after the date because he did not want to scare her away or seem too eager to start a relationship. When Alice received this message, she felt relieved since she was thinking why Bob did not text her after the date. She did not reply to Bob immediately, but after another two days. Alice made this decision because she also did not want to seem like she was being too eager to start a relationship.

From the example above, we can see that dating is a strategy game. The mindset of a person determines how a person chooses their strategy in order to get what they want. Alice and Bob both like each other after the date, but they spend about 4 days to confirm the status of their relationship. Think about if they both texted each other immediately after the date, they could have both confirmed their feelings towards each other and became a couple immediately after the first date. However, this is not always the case in real life since we do not know how the other person is thinking. A rational person always tries to be safe and avoids unfavorable situations. In the case of dating, being too eager in a relationship might scare the other away.

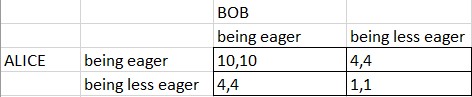
If we construct a payoff matrix according to their situation, we can see that Alice and Bob are facing the Prisoner’s dilemma. Since both of them do not want to seem eager to each other, they both have a lower payoff. This means that they spent unnecessary time on playing mind games with each other (represented as (1, 1) in the payoff matrix) to reach the same result had they both chosen “being eager” (to start communicating immediately after the date). We can see that this scenario illustrates a breakdown of communication between Alice and Bob. The lack of cooperation and overly considerate behavior between the two leads to a situation very similar to the Prisoner’s dilemma, and they do not really have a dominant strategy since they cannot know what the other is thinking. If they talk openly, maybe they would end up in a better Nash equilibrium of (10,10), but not (1,1) (Figure 2).

In conclusion, dating apps are a modern way to meet people and find your love. However, people tend to be cautious when they pursue people that they like, which creates such a situation that might result in one very similar to the Prisoner’s dilemma.

---

References:

• https://fee.org/articles/coase-theorem-the-prisoner-s-dilemma-and-zero-sum-games-in-modern-dating/
• https://qz.com/996851/why-we-need-a-dating-app-that-understands-nashs-equilibrium/
• https://generic.wordpress.soton.ac.uk/meetingofminds/2018/03/22/game-theory-matching-apps-as-social-networks/
• https://www.britannica.com/science/game-theory/The-prisoners-dilemma

Do you trust your friends? I know it is obvious that your response will be, “Of course I trust them! Why would I not?”. Yet, take this to the perspective of social networks or communication on digital networks and you might change your mind.

Paulo, the author of Introduction to Cyber-Warfare, states that there are dangers in transitive trust, which is a topic that is covered in class. Transitive trust is when User A trusts User C under the condition that User A trusts User B and User B trusts User C (see Figure 1). This creates a triadic closure among the three users. We will assume that the direct trust is a strong tie, and the transitive trust can be either a strong or weak tie. Paulo references an experiment performed by Thomas Ryan, in which he observes how a fake account spread through social networks and got people to trust it through transitive trust. Ryan created a fraudulent account called “Robin Sage” with made up information and put her profile on LinkedIn, Facebook and Twitter. This experiment provides some interesting results.

Ryan quotes one user messaging “Robin Sage” stating “I’ve never met you, but I saw you had Marty on your Facebook list, so that is good enough for me.” This shows a common action on social media which is that people tend to send friend requests to those who have mutual friends with them, which is a form of transitive trust common on social media. Another type of transitivity is when a person has a lot of connections with highly respected or trustworthy people. People tend to trust that person, even though they have never met or talked to each other in real life. In the experiment, “Robin Sage” has an extraordinary profile on social media platforms, having graduated from MIT and boasting NSA internship experience. Her extraordinary profile allowed her connect with Joint Chiefs of Staff, the CIO of NSA, etc. – which allowed her to gain the trust of many people through a cascading effect.

Another interesting thing Paulo references is the “tipping” model, introduced by Laureate Thomas Schelling. This model clearly points out that when there are two people believing or following a trend, their mutual connection will eventually believe or follow that trend as well. The following graph can give you an idea on how your friends who you trust can eventually influence everyone on what they believe.

Let’s go back to Ryan’s experiment. If we apply the “tipping” model on that experiment, provided that there is a network that indicates their connection (nodes are users, and edges between them means they are friends, or they trust each other), then, from the above diagram, a shaded node represents a user that trusts “Robin Sage” as a legitimate person, which is an effect that cascades throughout the network. From box 1, we can see there is a white node that trusts two gray nodes. The two gray nodes can then convince the white node to trust “Robin Sage” as a legitimate person, due to the “dipping” model. This action repeats recursively within the network, and eventually the whole network will believe that “Robin Sage” is a real person, even though they have never met her in person. This spread in the network is justified by the Strong Triadic Closure property.

As an analogy, consider a scenario where one person tries to spread a false message and one of your friends trusts his/her word. Your friend will bring that message into your network and gradually spread it to everyone. You cannot easily determine if the message is true or not, but since your friends trust it, you will generally trust them.

The PGP web of trust is a real world example that has this kind of issue, where you can never know if your friends trust the right person. It is dangerous to trust your friend on the Internet without really knowing them, in the perspective of the web of trust. If one of your friends trusted a malicious person, by the transitive trust property learned in class, you will trust the fraud as well. Transitive trust in PGP may bring us the convenience of quick verification but it also creates potential trust issues in the network. The best practice when dealing with trust online is only to trust people that you really know in person, and to exchange your PGP keys in a secure way.

So, ask yourself again: Do you still trust your friends on the digital network?

---

Citations:

• Shakarian, Paulo, et al. “Chapter 9 – Losing Trust in Your Friends: Social Network Exploitation.” Introduction to Cyber-Warfare: a Multidisciplinary Approach, Syngress, 2013.
• Herald, Sarvjeet et al. “A non-transitive trust model for key distribution.” (2010).
• https://medium.com/@bblfish/what-are-the-failings-of-pgp-web-of-trust-958e1f62e5b7
• https://www.csoonline.com/article/2633175/be-careful-with-transitive-trust.html