If aliens exist, why haven’t we seen them yet? After all, the universe is vast, and Earth-like planets are abundant. This is the Fermi Paradox, which says that it is a contradiction that while alien life should be plentiful, we have yet to make contact with any of them.

One possible explanation for the Fermi Paradox is the “Dark Forest” theory, which models the vast universe as a “dark forest” and civilizations as “hunters.”
To understand this, the theory requires three axioms to be assumed as true:
- Every civilization wants to survive.
- Every civilization wants to expand and grow.
- Every civilization is either friendly or hostile.
From axiom 1, every civilization would do anything to ensure the survival of their species.
From axiom 2, every civilization advances their technology over time. This also means that civilizations advances their weaponry over time. (A famous example of this is shown in the amazing match cut in the film 2001: A Space Odyssey, shown below.) However, not all species would advance at the same rate, and so some civilizations may be more advanced (and thus powerful) than others.

From axiom 3, every civilization can be categorized as either hostile or friendly. Friendly civilizations would try to form an alliance with other civilizations and join forces in the spirit of collaboration. Hostile civilizations would destroy any civilization it comes across, deeming them as dangers to their own survival.
Suppose civilization A discovers civilization B. Civilization A cannot be sure if Civiliation B is friendly or hostile, but it knows that civilization B has a probability P of being both hostile and more technologically advanced then A. Similarly, if civilization B discovers civilization A, it knows that civilization A has probability Q of being both hostile and more technologically advanced than A.
We can model this situation in a payoff matrix, where either civilization can either destroy or ignore the other.
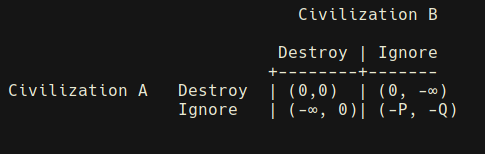
Since the values of P and Q are unknown for each civilization, the only clear Nash equilibrium here is to (Destroy, Destroy), which means it is better to preemptively destroy rather than risk being destroyed. In essence, the universe is a “dark forest” where every civilization is a hunter trying to keep quiet. If discovered, hunters have only one thing they can do, which is eliminate the others, in order to ensure survival.