CSCC46 Blog 2019

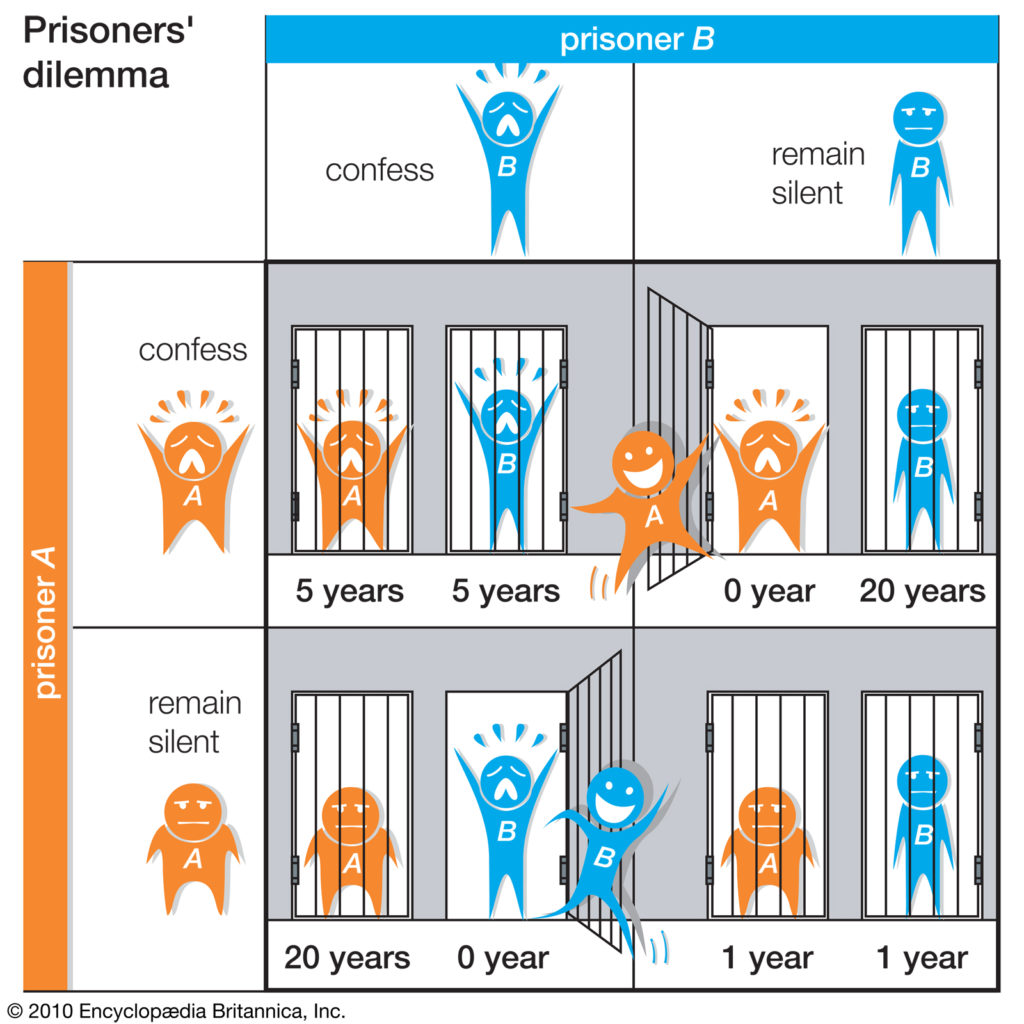
A business cartel is formed when more than one competing businesses in a market decide to coordinate with the goal of fixing prices to be higher than normal so that consumers must pay more for their products; this typically occurs in an oligopoly. A successful cartel is able to act almost essentially as a monopoly in the market.

Let me define a few terms first:
Monopoly – A market with pretty much only one producer and is thus able to dominate and set prices (think of the LCBO)
Oligopoly – A market with only a few, but big players (think of the Canadian banks)

As you can see just by this definition, a lot of game theory is involved in the process of forming a cartel. Do we compete? Do we collude? If we decide to collude, how do we know the other won’t cheat? Aside from regulations, this paranoia that the other business may decide to cheat is also what holds competing businesses back from colluding, even though they would both benefit much more by colluding.

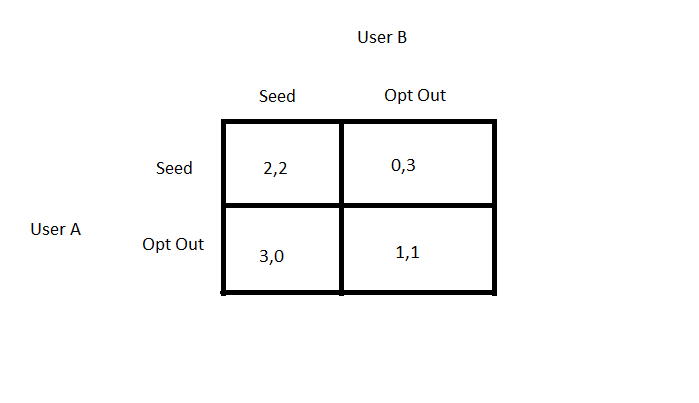
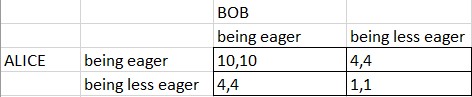
Let’s take a look at an example, suppose we have business A and business B competing with each other. For this model, we will also have to assume that the product or service they are offering is exactly the same and that they are the only two businesses in the market. At the moment, these businesses are making a profit of 5 million dollars per year each. If they decide to collude, they can hike up the prices and will both make 10 million dollars per year each. However, any one of the businesses could decide to cheat and lower their price or produce more. Now, more consumers will be buying their product instead and they make 12 million dollars per year while the other business only makes 3 million dollars per year. The payoff matrix looks like this.

The model is simple and requires some unrealistic assumptions, but it also reflects what could happen in reality to some extent. If the businesses colluded, they would both make a total of 20 million dollars per year, making the businesses very happy. While if they both competed, they would only make a total of 10 million dollars per year, making the consumers happier. In the middle, we can see if one business cheats while the other collaborates, the one that cheated makes a huge amount of profit compared to the other. As you can see, this looks like the classic prisoner’s dilemma problem and both business’ best response is to cheat no matter what the other business decides to do. Thus, the single Nash equilibrium of this problem is for both businesses to cheat. Overall, game theory, which is part of the course content, gives us some insight as to why businesses would rather compete than collude (other than the fact that colluding is illegal).

Reference

Understanding a Cartel as a Prisoner’s Dilemma. (n.d.). Retrieved November 12, 2019, from http://college.cengage.com/economics/0538797274_mceachern/student/transcripts/8432.pdf.

Boxing is a fighting sport where the goal is to harm your opponent to achieve a higher score. Boxers have to condition their body on a regular basis to increase their fighting skills in speed, power and technique. If you have watched any professional boxing match, you would know how intense the fights can get. In most matches, the boxers’ faces would have taken so much damage they start bleeding.

Given this situation, the way to win is to land as much punches to their opponent’s face and body. However, if the opponent knows this, he will choose to avoid damage and try to deal damage of his own. In the boxing ring, a boxer can do one of the four actions: attack, defend, maneuver or observe. These choices apply Game Theory and is an instance of the Zero Sum situation.

When a boxer attacks, he can be nullified by a block. The attacker will lose some energy while the blocker sustain much lesser to no damage. Attacks can also be negated by a maneuver, making the attacker waste energy, balance and sight.

When a boxer defends, he will prepare for an attack but would reduce his sight.

When a boxer observes, he is looking for a perfect opportunity to attack, increasing his accuracy and critical hit chance.

It is not hard to infer from the title of Pasquinelli’s article “Google’s PageRank Algorithm: A Diagram of the Cognitive Capitalism and the Rentier of the Common Intellect”, that he views the PageRank algorithm as a structure of Cognitive Capitalism. He explains that by mentioning a link in an article or even clicking on a hyperlink, each individual who uses the search engine contributes their knowledge and opinions to make the machine more intelligent, efficient and beneficial to others. Assuming that the majority of the people using Google have good intentions, we have a “wisdom-of-the-crowds” effect: the more a page is referenced, the more people consider it to be significant, the more value other people will potentially acquire from in it. As an effect, the pages which already have a high score keep growing it at a faster rate, because they are more likely to be visited and referenced in the future than pages with a lower PageRank.

It is quite simple to draw a parallel with how people become billionaires. According to Investopedia, the most common ways people become billionaires are through “inventing, investing, innovating and being an entrepreneur” (or a combination of such).

If we apply PageRank analysis to the dynamics of economic ranking in a capitalist society, we can see that the reason why people become billionaires in the first place is because they have generated something that was deemed valuable by many people who are willing to partake in transactions to acquire benefits from such innovations, as a result of which, the billionaire generates more revenue. “Cognitive Capitalism” also plays a role in placing billionaires in their positions of power: the more people engage in financial transactions with them, contributing to their wealth, the more they demonstrate their trust and approval of the billionaire’s endeavors, the more other people are willing to contribute their trust and resources, giving the billionaire a bigger platform.

As seen in lecture, some certain structures of a network could cause the Basic PageRank algorithm to unfairly accumulate PageRank in a cluster of nodes which have no edges going out, back into the rest of the graph. Although many other nodes could have lots of in-links and be valuable resources, they would end up with 0 PageRank score. This is why the Scaled PageRank algorithm introduces a scaling factor to redistribute the score among all nodes evenly, and this results in a more accurate score for all nodes.

Now imagine we lived in a pure capitalist society where no one paid taxes. We could easily run into the same issue as with the Basic PageRank algorithm, where all the wealth piles up in the wrong places. Therefore, in my opinion, it is unimaginable to live in a purely capitalistic society due to the issues with our socio-economic network structure. There needs to be a well balanced “scaling factor” applied to everyone (for PageRank, a stable scaling factor is considered to be between 80~90%). However, overtaxing would also be wrong. Imagine increasing the scaling factor in PageRank more than necessary: the greater the scaling factor, the more likely people will get the wrong sources mixed in with the right ones each time they search. Wisdom of Crowds is a legitimate phenomenon, from which everyone benefits, so some sense of hierarchy is essential to avoid giving irrelevant resources too much power.

However, the real economic network is not as simple in reality as can be depicted on a graph. I will end this blog with one such fact: according to the Business Insider, “The equivalent of 10% of world GDP is held in tax havens globally”. Above is a graphical representation of how much wealth in some countries is held in offshores to avoid paying taxes in proportion to the country’s GDP, which prevents a fair distribution of wealth in the world. (Taken from BusinessInsider, linked in references)

So, should billionaires be paying more taxes? Coming from a network analysis perspective, my answer to that is they should pay the taxes on all their wealth, including what is held in offshores, so that the wealth distribution would not be so skewed and each economic entity in our social network would have an accurate net worth, proportional to the benefit they bring to society.

References:

Mueller, Annie. “7 Real-Life Ways to Become a Billionaire”. Investopedia, updated Jun 25, 2019. Accessed Nov 12, 2019.
https://www.investopedia.com/financial-edge/0311/7-real-life-ways-to-become-a-billionaire.aspx

Pasquinelli, Matteo. “Google’s PageRank Algorithm: a diagram of cognitive capitalism and the rentier of the common intellect”. Published by Pankov Mar 16, 2010. Accessed Nov 12, 2019.
https://pankov.wordpress.com/2010/03/16/google%E2%80%99s-pagerank-algorithm-a-diagram-of-the-cognitive-capitalism-and-the-rentier-of-the-common-intellect

Nicolaci da Costa, Pedro. “The ultrawealthy have 10% of global GDP stashed in tax havens — and it’s making inequality worse than it appears”. BusinessInsider, Sep 13, 2017. Accessed on Nov 12, 2019.
https://www.businessinsider.com/wealthy-money-offshore-makes-inequality-look-even-worse

Much of today’s entertainment takes on a digital form; movies, music, games, and other digital goods. Naturally, in this day and age where network access is considered an essential service and almost everybody owns a personal computer, Torrenting is one of the most convenient ways to share content (both legally and illegally). Torrenting sites are very useful in that they gather content and allow everybody to access all this content, whether it is recent content or content that was released a long time ago. However, not everybody has a fast (or unlimited data) internet connection. Especially in Canada, where data plans are criminally overpriced. For Torrenting to work, we must have “seeders” (users who are uploading the data) in order for “leechers” to be able to download a file. The more seeders a file has, the faster a leecher is able to download the data. Typically, a user would download the file they want as a leecher, and then contribute afterwards as a seeder. The new seeder will then help increase the download speed for the next leecher, who will then join as a seeder, and so on. The problem that arises is the fact that a user is not obligated to become a seeder; a user may choose to download the file and opt out of being a seeder, as seeding uses up data and may slow down your connection while seeding. Then, why would anybody become a seeder? Game Theory helps explain why.

Suppose there were 2 users looking to torrent files. Torrenting a file would give 2 points of satisfaction, while saving up data/bandwidth is worth 1 (since they decided that it is worth using data to torrent). Then, they would both be better off seeding than if they were to both opt out. However, this is not the Nash equilibrium, as if user A opted out from becoming a seeder and user B becomes a seeder, then user A gets to download the file that user B uploads while using minimal bandwidth/data (which can be utilized elsewhere, such as torrenting more files) for a total of 3 points of satisfaction. User B on the other hand would not be able to download without a seeder, in addition to using up data themselves to seed for others. The same can be said if user B opted out, and user A becomes a seeder. At this point, the user that seeds realizes that they’re better off opting out as well, as even though neither would have the files they wanted, using up bandwidth for something else is better than being purely leeched off of). This would mean that all torrents are essentially dead, with nobody to upload.

This is why many trackers implement a Share Ratio, which keeps track of how much data a user uploads, versus how much a user downloads; a user with a lower share ratio risks getting blacklisted (and thus unable to download). This changes the payoff matrix.

Previously, opting out allowed to gain 2 points of satisfaction from torrenting, plus 1 point of satisfaction of using remaining bandwidth for something else. Now, in the long run, opting out and being blacklisted would prevent them from gaining the 2 points of satisfaction. This gives incentive for users to become seeders, allowing torrenting to become self regulatory. Because the Nash equilibrium is now for users to seed for eachother, the system becomes sustainable, and introducing punishments (such as fines) would be the only way to prevent illegal torrents.

https://globalnews.ca/news/4933339/lawsuits-movie-downloading-uploading/

https://blogs.cornell.edu/info2040/2012/09/18/applications-of-game-theory-in-the-bittorrent-protocol/

In today’s modern day, people are connected with other people; not just in school or at the workplace, but also on the Internet. There are various popular social applications such as Facebook, Twitter, and Instagram which allow us to get in touch with our friends. With the introduction of online dating in social networks, people are able to find romantic partners online in ways never imaginable before. However, the communication will be most likely happen on the Internet, which gives people the option to meet up in real life only if they are comfortable in doing so.

This topic is relevant to the study of Game Theory, which we covered in class with some examples about how two people (or groups) will select a strategy that provides the highest payoff or benefits. Most people, if they are rational, will choose the best strategy based on what other people choose (i.e. dominant strategy). In the perspective of dating app users, the following example below illustrates the mindset of when they engage in a conversation with another user, which relates very closely to the Prisoner’s dilemma that was also covered in class.

Alice and Bob are users on a dating application and they found each other on the application, wanting to know more about each other. Bob initiates the conversation and they both have a good time talking. Later on, they decide to go on a date, and it goes great. They both feel good about each other and they now like each other, but none of them have asked the other to confirm their current status. Moreover, they did not text each other after the date. After two days from the date, Bob finally decided to ask Alice if she wanted to hang out with him. He did not contact Alice after the date because he did not want to scare her away or seem too eager to start a relationship. When Alice received this message, she felt relieved since she was thinking why Bob did not text her after the date. She did not reply to Bob immediately, but after another two days. Alice made this decision because she also did not want to seem like she was being too eager to start a relationship.

From the example above, we can see that dating is a strategy game. The mindset of a person determines how a person chooses their strategy in order to get what they want. Alice and Bob both like each other after the date, but they spend about 4 days to confirm the status of their relationship. Think about if they both texted each other immediately after the date, they could have both confirmed their feelings towards each other and became a couple immediately after the first date. However, this is not always the case in real life since we do not know how the other person is thinking. A rational person always tries to be safe and avoids unfavorable situations. In the case of dating, being too eager in a relationship might scare the other away.

If we construct a payoff matrix according to their situation, we can see that Alice and Bob are facing the Prisoner’s dilemma. Since both of them do not want to seem eager to each other, they both have a lower payoff. This means that they spent unnecessary time on playing mind games with each other (represented as (1, 1) in the payoff matrix) to reach the same result had they both chosen “being eager” (to start communicating immediately after the date). We can see that this scenario illustrates a breakdown of communication between Alice and Bob. The lack of cooperation and overly considerate behavior between the two leads to a situation very similar to the Prisoner’s dilemma, and they do not really have a dominant strategy since they cannot know what the other is thinking. If they talk openly, maybe they would end up in a better Nash equilibrium of (10,10), but not (1,1) (Figure 2).

In conclusion, dating apps are a modern way to meet people and find your love. However, people tend to be cautious when they pursue people that they like, which creates such a situation that might result in one very similar to the Prisoner’s dilemma.

References:

• https://fee.org/articles/coase-theorem-the-prisoner-s-dilemma-and-zero-sum-games-in-modern-dating/
• https://qz.com/996851/why-we-need-a-dating-app-that-understands-nashs-equilibrium/
• https://generic.wordpress.soton.ac.uk/meetingofminds/2018/03/22/game-theory-matching-apps-as-social-networks/
• https://www.britannica.com/science/game-theory/The-prisoners-dilemma

Game Theory can be used to explain the inherent bias in some games that are presented as fair. The Skin Game, a card game where 2 players present cards and are rewarded based on the resulting cards, is inherently biased towards Player 1 and this bias can be shown with a payoff matrix. In the Skin Game, each player is given an ace of diamonds and an ace of clubs, Player 1 is given a 2 of diamonds and Player 2 is given a 2 of clubs. Both players select one card to show without knowing the opponents choice and the cards are then compared. Player 1 wins if the suits match, Player 2 wins if the suits don’t match and if both players present the 2’s, the payoff is zero for both. The below payoff matrix describes the Skin Game.

Based on the above payoff matrix, we can see that Player 1 is advantaged if they never choose the ace of diamonds, while choosing the ace of clubs 60% of the time and the 2 of diamonds 40% of the time to remain random. With this setup Player 1 can expect to win 0.2 points per round. This simple game clearly has a strategy that can help a knowledgeable player make money. Games like these are used all over the world to make money from unsuspecting players, so learning Game Theory can help save you money.

Resources:

https://www.scientificamerican.com/article/what-is-game-theory-and-w/

While it is easy to assume that when looking at all of the websites on internet that most of them should have a low page rank, as there are hundreds of millions of websites and a small minority of them are known by a majority of the users, there needs to be analysis on the links between websites to be sure.

To reach a definite conclusion to this, data analysis was performed on 2 billion edges of 90 million hosts, where the edges are links from one host to another. It is important to note that page rank is dependent on the number of links and the quality of those links that a host receives, rather than the number of links it has to other hosts.

Some intersecting details about the Common Crawl data is that the host that receives trhe most hosts is googleapis.com, the host that sends the most links is blogspot.com, and the host that has the most subdomain, hosts that are part of a larger host, is wordpress.com.

This topic is related to the course because it shows that subdomains of a domain can be considered strongly connected components because all the subdomains have links that go to and from the domain, so all the subdomains are connected together.

https://searchengineland.com/crawl-data-analysis-of-2-billion-edges-from-90-million-domains-offers-glimpse-into-todays-web-323417

I’m a big fan of the concept of the Balance Theory concept that we learnt earlier in this class. The idea that given a complete graph K_3, that only the following signed edges are considered balanced: +++, -+-. In my previous article, we explored how Balance Theory can be applied to relationships (in a TV Show nonetheless), and I ended off talking about how it would be interesting in to see how this can be applied to politics.

I think politics can be seen similarly to drama and relationships in this sense. Countries that cooperate with each other or countries that are considered to be “stable” can be seen as balanced edges, while conflict, either between countries or within a country, can be seem as unbalanced edges. Although it may be a stretch, I also think a political deadlock such as the UK over the Brexit process can be similarly analyzed just as Friends was analyzed. The process is not moving forward smoothly due to conflicting incentives, resulting in party infighting, infighting within British parliament, and friction between both the British People and their Representatives in Parliament.

So when looking for an article to write about for this blog post, I was skimming the Wikipedia page for Balance Theory where I noticed that it gave an example of the Theory being used through Celebrity Endorsements. This made sense, in that, if a viewer were to see a celebrity that they liked endorsing a product, they would be moved to also take interest in that product. This also meant that if the viewer did not like the celebrity endorsing the product, they would also develop disdain for the product. This sort of logic could be the explanation for the partisanship we see today, in modern politics.

I also ran into this journal: https://journals.sagepub.com/doi/pdf/10.1177/1532673X8100900303. It’s about the analysis of applying balance theory between voters, political issues and Gerald Ford. After the data has been collected, it is shown that the predictions that Balance Theory would suggest are probable.

It is well known that after struggling through first year at UofT, students are then granted admission to their preferred Program of Study (POSt) only if they pass certain criterion.

At UTSG, the top X% of students are admitted to the CS POSt. This means the students are directly competing with each other for the limited spots in the program. At UTSC, students with a cumulative GPA greater than 3.0 (~ 75%) will be admitted to the POSt. Comparatively, this means that students at UTSC gets admitted into the CS POSt independently of each other.

Let us first consider a fictitious simple model that can represent the UTSG CS POSt admission game. Suppose that there’s only one space available for the CS program and Alice, Bob, and Charlie are the last contenders to be considered. If each of the three of them decide to study, then they each have a 33.3% chance of making it to the program. However, they could also choose to sabotage another student. Suppose that Alice and Bob are enemies, if Alice decides to sabotage Bob, then Bob’s admission likelihood would decrease to 10%, and Alice’s likelihood raises to 40% (this implies Charlie’s likelihood gets raised to 50% and it makes sense since Alice didn’t spend time to study for her exams!). If Alice and Bob both decide to sabotage each other, then they will split the 50% that’s left over (Charlie again has 50% chance) which gives them 25% each.

UTSG POSt Game

Given the set up, it is easy to apply the game theory analysis to this game. As a student, you can either choose to study or sabotage student such that you gain some advantage over the other. Here it is clear that regardless of what the other student does, sabotaging will yield a higher score. Thus, sabotaging is actually the dominant strategy for both Alice and Bob. If we suppose that Alice and Bob are logical enemies and they follow the rules of game theory, then they would adopt to their dominant strategy. This is clearly a ridiculous outcome, as it would make more sense for students to sabotage each other than to study!

Now let us consider the following fictitious UTSC CS POSt admission game. Where the admission likelihood of any student is independent of other students.

UTSC POSt Game

The difference at UTSC is that sabotaging other does not increase your chance of being admitted to the POSt. On the contrary, since you’re not studying, then you actually lower your chance. Again, applying game theory analysis to this game, the dominant strategy for both Alice and Bob would be to study. This should be the expected behavior of students at a University.

To summarize, I argue that the UTSC CS POSt method is one that is better than UTSG’s in terms of what is the expected outcome from their respective students. On one hand, the UTSG POSt creates a “zero-sum thinking” environment where students think that in order to achieve success, others must suffer. While at UTSC, students will more likely to work, study, and help each other to improve their own chances of getting accepted, and during that process also elevate their peers.

Resources:

https://en.wikipedia.org/wiki/Zero-sum_game
https://en.wikipedia.org/wiki/Zero-sum_thinking
https://journals.sagepub.com/doi/10.1177/0022022115572226
https://atrium.lib.uoguelph.ca/xmlui/handle/10214/10034

Rangers and poachers are constantly fighting a cat and mouse game. The poachers trying to set snares to capture sought after animals, and the rangers attempting to apprehend them. After numerous unsuccessful attempts to combat this behavior, the Indian government, with the help of the University of Southern California, developed the Protection Assistant for Wildlife Security (PAWS). The goal of PAWS is to determine patrolling routes to increase the effectiveness of the anti-poaching. To do this, PAWS uses a mixture of artificial intelligence and game theory. This is a great application for game theory, as there is a clearly defined adversarial relationship; the poachers are constantly switching up their routes, trying to evade the conservationists and the conservationists are trying to stay one step ahead of the poachers. Using previous poacher and ranger activity, along with animal population data, map data, and many other constraints, PAWS creates a model of the poachers’ behavior. Exploratory PAWS patrols have lead to almost double the number of average human sightings, demonstrating the clear predictive power of the algorithm.

I like this example because it highlights how applicable game theory is to many real world situations. We are constantly bombarded with these sorts of adversarial relationships and this article inspires me to search for places in my life where I could use this understanding to more effectively respond to the situation. From modelling competition in the marketplace, soldiers on the front line, to poachers, game theory, no doubt, deserves all of the accolades it has received.

References:

• https://www.cais.usc.edu/wp-content/uploads/2017/07/Fang-et-al-IAAI16_PAWS-1.pdf
• https://analyticsindiamag.com/ai-game-theory-can-now-predict-where-poachers-are-likely-to-strike-next/