Reference journals:
https://pubs.aeaweb.org/doi/pdf/10.1257/jep.30.1.185
https://www.sas.upenn.edu/~fdiebold/papers/paper39/ABDE.pdf
For purposes of maximizing profits and minimizing risk in stock markets, many traders seek to model the stock market as accurately as possible. Recently (<100 yrs), index investment has grown in popularity over investments in individual stocks (index investment is a strategy of investing in a broad market or range of stocks). The reason can be explained using power laws.
In almost every major market benchmark such as the S&P500, the top 20% of stocks, in terms of market cap and trade volume, represent approximately 85% of the total market size. More interestingly the same pattern appears in the distribution of market returns. The top 20% of stocks represent approximately 80% of the market’s year-on-year return (on average). This inequality is graphically similar to the long-tailed graphs we saw in class; in other words, the distribution of returns in the stock market is a long-tailed power law distribution. And according to the author’s research, it is in fact consistent with
P(x > X) ~ 1/X^a , with a = 3 : an inverse cubic power law
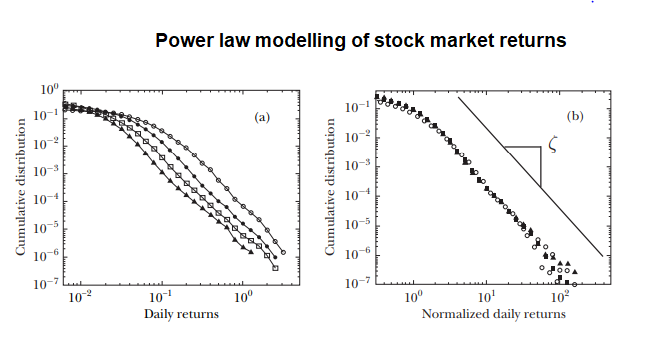
This formula is consistent with the one we discussed in class: p(x) = x^-a. It is also consistent with our discussion of the value of alpha (the a value) which we discussed to mostly be 2 < a < 3 . This is interesting but why is it important? This is important because since stock markets follow power law distributions instead of something like a Gaussian, extreme variations in day-to-day prices (such as crashes) are very rare. Because of the cubic law behavior of markets the chances of a stock price deviating from the mean by 10% is 1000 times less than if market returns were instead Gaussian. And we can see this in practice, on average only 1 out of 1000 stocks on any given day on the NYSE deviate by 10% (which means the market is relatively stable, which is good).
This modelling of power laws is also leads to strategies for trading. Traders can either aim to pick or not pick the stocks that tend to deviate more. In a good economy, perhaps they will pick the few stocks that are on the extreme tail of the power law distribution, and oppositely in a bad economy. Example being in 2015 when the S&P500 would have ended the year with negative growth if it were not for 10 stocks and F.A.N.G (FANG = Facebook, Apple, Netflix, Google). Conversely, during the tech bubble burst, you would not have wanted to pick these stocks. In class we briefly discussed models that lead to power laws. It turns out that the random walk model is what makes stock returns a power law distribution.
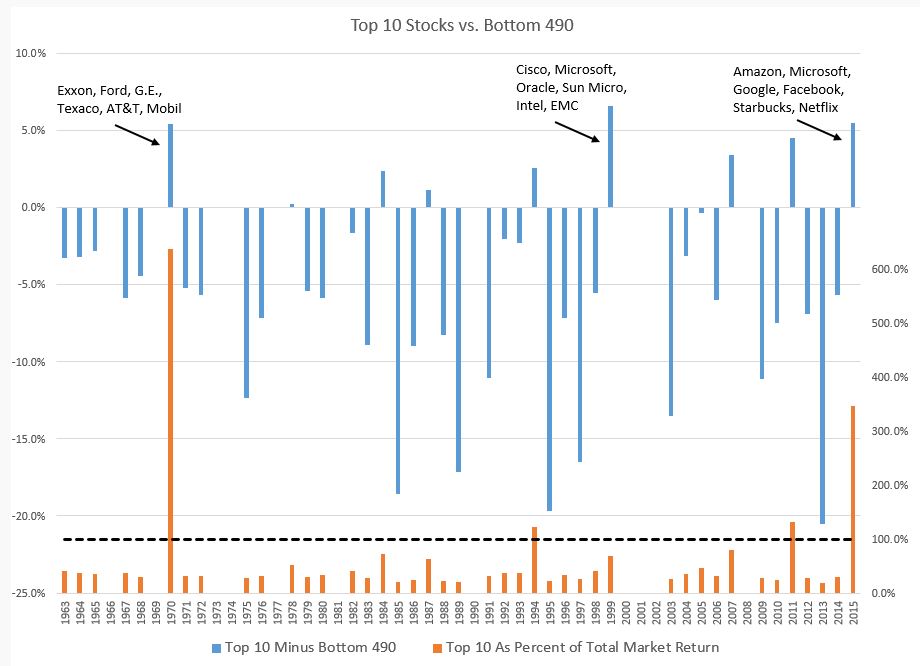
Going back to why index investment is gaining popularity — because according to the distribution of market returns, it is safer to diversify instead of pinpoint specific stocks. Investing in stocks from the tail (extreme deviations) only works when times are good, and because it is very difficult to predict good/bad times, money managers often make the safe play of diversifying (game theory!).
Overall it is interesting to see how the theory of power laws we covered in class are represented in society because sometimes it is not immediately obvious as to why power laws would model certain things — such as the stock market since for the most part the market grows and shrinks randomly.
Reference List
Gabaix, Xavier. “Power laws in economics: An introduction.” Journal of Economic Perspectives 30.1 (2016): 185-206.
Andersen, Torben G., et al. “The distribution of realized stock return volatility.” Journal of financial economics 61.1 (2001): 43-76.

