“Speedrunning” all UTSC Computer Science Courses Using Graph Theory

Motivation

Imagine a UTSC student S. He loves computers, he loves them so much to the point that he wants to take every single computer science course available at UTSC. He wants them done as soon as possible so that he could get his diploma quickly and move on. Suppose he has infinite brain power and can take an infinite number of courses each term, what is the shortest possible time for him to finish all computer science courses at UTSC?

He certainly couldn’t take all courses at once, because for most courses there exist a set of prerequisite courses, which has to be finished first before taking the course. We can represent this relationship using a graph. If course A has prerequisite course B, then we can have courses A and B as nodes, and create a directed edge from A to B. Based on this premise we can build a graph representing ‘prerequisite-ness’ relationship among all computer science courses.

The Graph

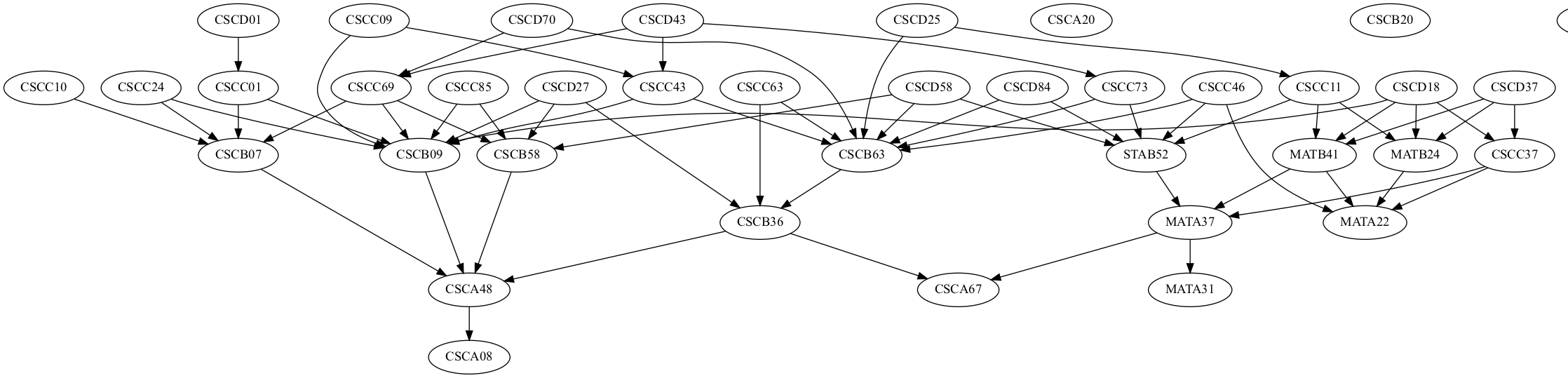
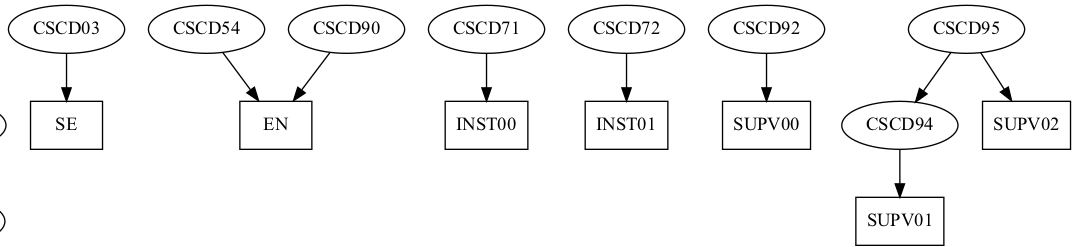(It’s recommanded to view these images in a new tab)

With the help of Python and Graphviz, I was able to visualize the network of computer science courses <1>. Observing this graph alone reveals a lot of information. We can see a giant connected component consisting of the majority of CS courses. This is expected because computer science knowledge is highly dependent on each other. In this component, courses CSCB09 and CSCB63 have the largest in-degree of 8, meaning these two courses are the most ‘directly depended on’ courses. On the other hand, the disconnected courses do not directly depend on any other courses in the network. They are mostly special courses<2> open to a selected set of students e.g. students in a specialist stream, with the exception of CSCA20 and CSCB20. These two courses are generic introductory courses targeting students outside the computer science program.

The Solution

Back to the problem. My intuition is to construct a BFS tree from starting at the top D-Level courses. The tree will first cover all top level courses in its first layer(depth = 1). These courses have an in-degree of 0, meaning no courses are dependent on them, therefore taking them in the last term will not affect our goal of taking all courses. Then in each deeper layer cover all the prerequisites of the previous layer, all the way down to first year courses. 

The tree will need a root to start with. We will add a ‘graduation’ node G at the very top. This node will be dependent on all courses with an in-degree of 0, so that our S could take all the top level courses in his last term using his infinite brain power.

Again for simplicity reasons, we will focus on the giant connected component.

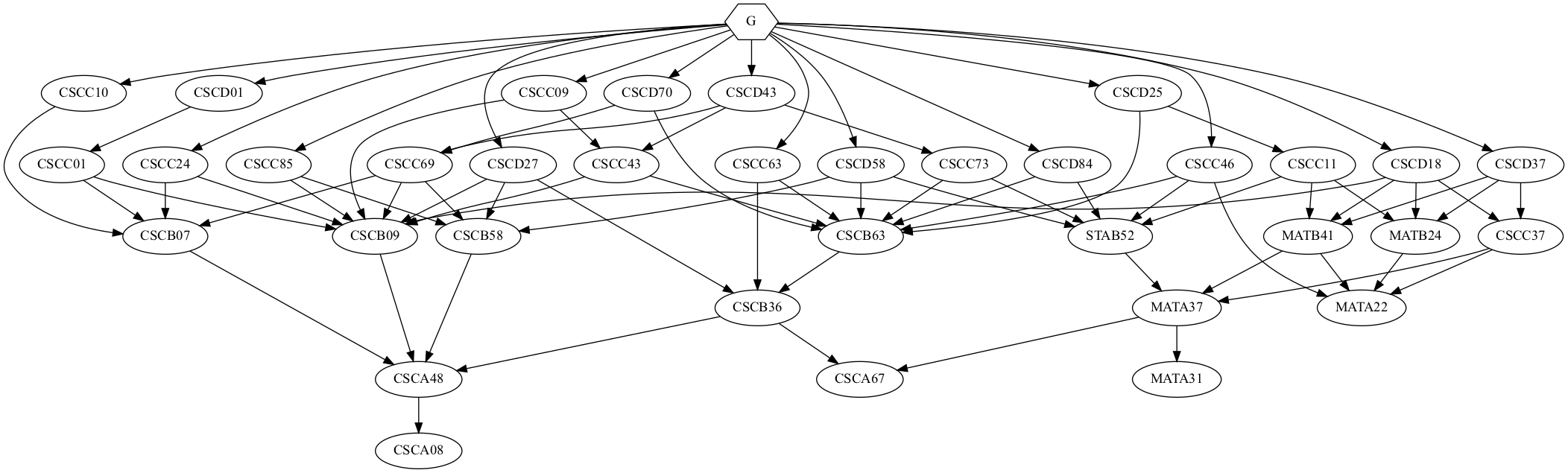
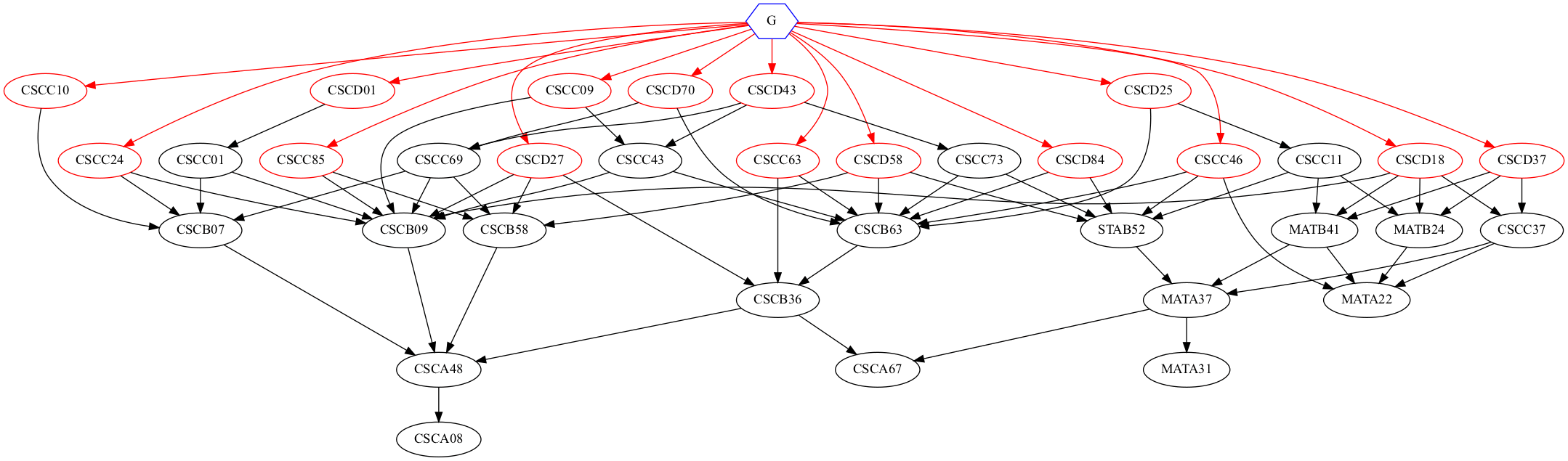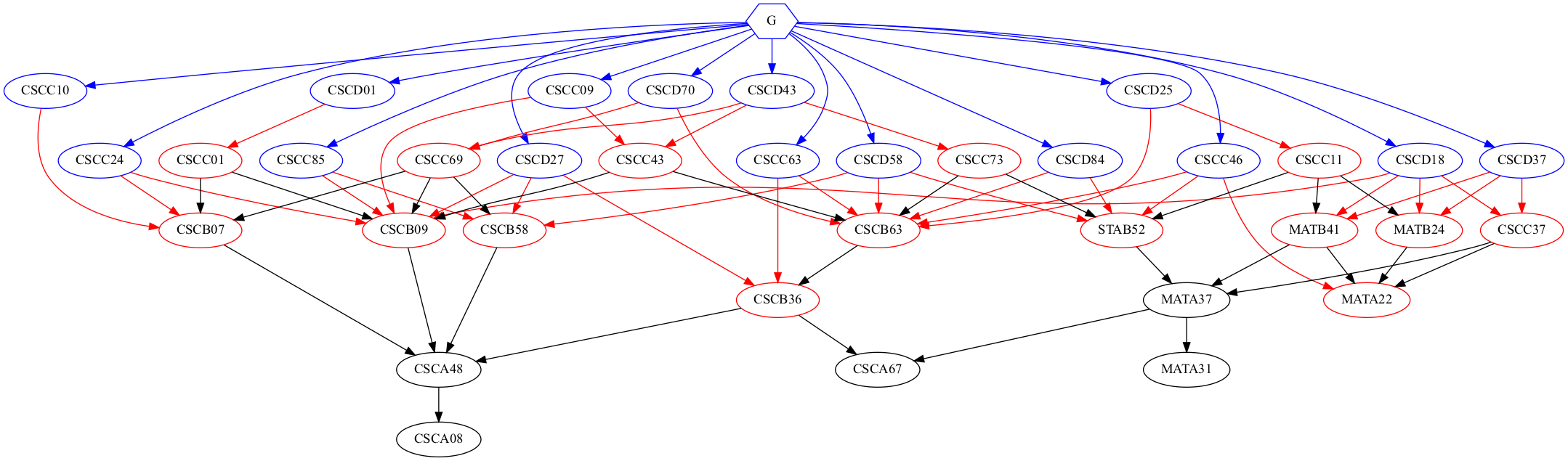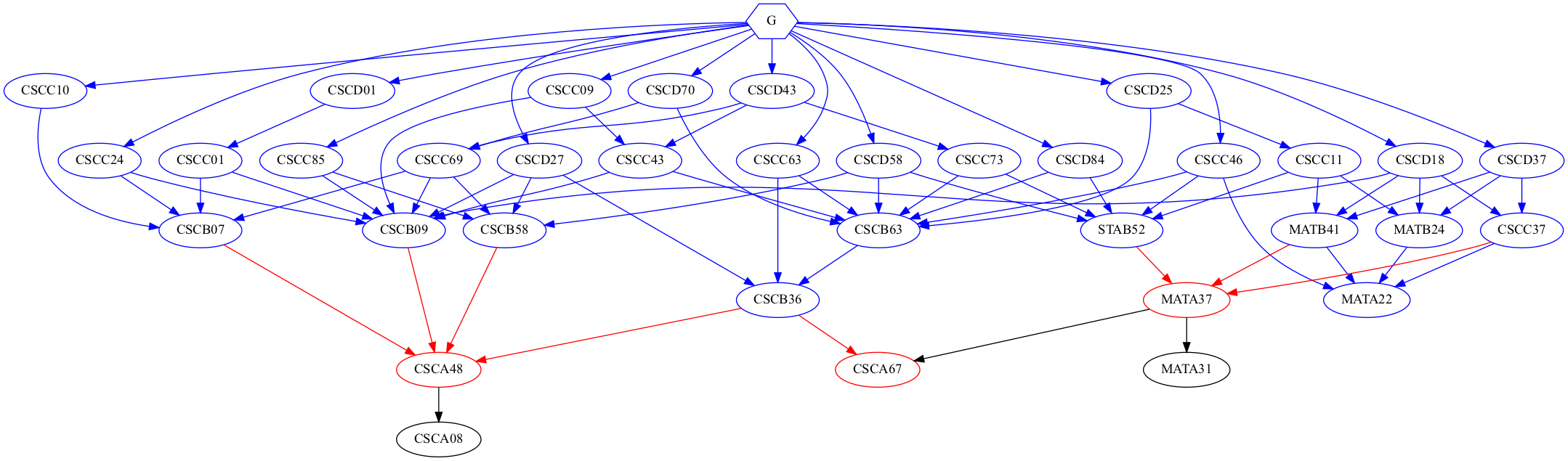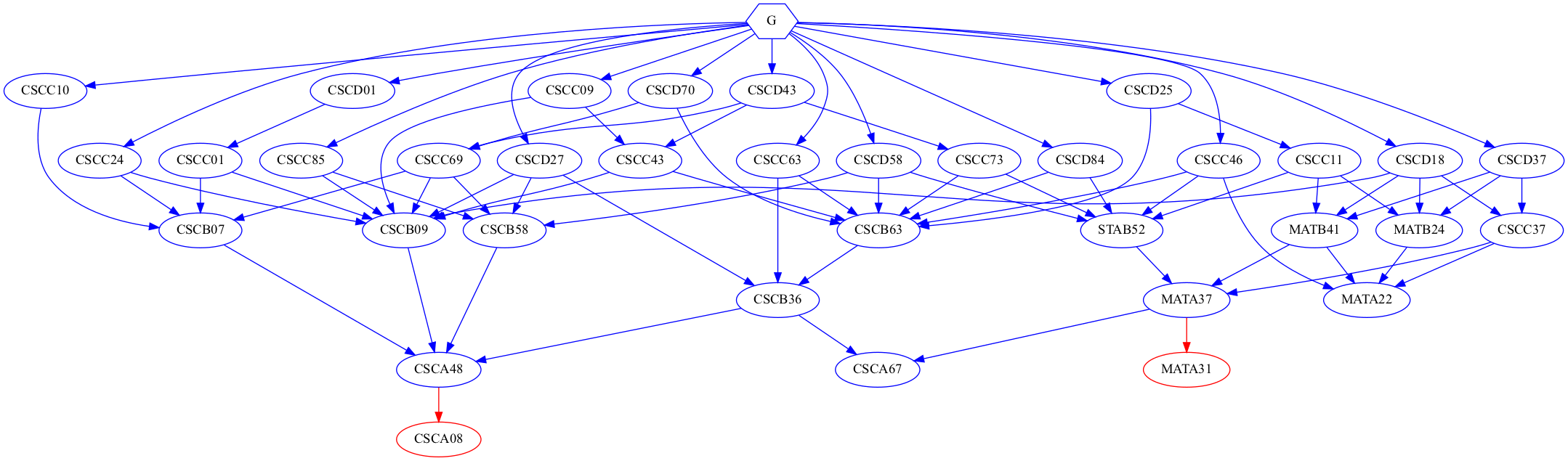
As we can see, every node is covered by the BFS tree with a height of 4. Therefore if S wants to, he can finish all CS courses at UTSC under 4 terms. 

Conslusion

Sadly, unlike S, we do not have infinite brain power. However, through this small experiment I realized that visualizing the course network as a graph does help clearing the mist for course selection and planning one’s path through a program. Therefore it would be a good idea to introduce an interactive visualization of the course network into the current degree explorer. 

Footnotes

<1>: This graph does not represent relationships like course exclusion and co requisites, these constraints only apply on a small subset of courses therefore for simplicity reasons we are ignoring these factors.

<2>: Rectangular nodes are ‘pseudo courses’ representing enrollment requirements other than the aforementioned factors. EN stands for The Entrepreneurship Stream, SE stands for Software Engineering Stream. INST** means a student needs the course instructor’s consent to enroll. SUPV** means a student needs the program supervisor’s consent to enroll.