The traveler’s dilemma, discovered by Kaushik Basu in 1994, is certainly one of my favorite of the game theory strategies that exist up to this date.
Why you may ask?
Well, let us first describe the game for those who are not aware of it.
THE GAME
The traveler’s dilemma involves two players who would like to receive a maximum payout. To make it more enjoyable to read, let’s say Tom and Jerry are your players and would like to get the higher payday compared to each other; fighting like always.
Tom and Jerry are both traveling when both their suitcases get lost and agree to get compensated between $2 to $100 by the airlines. However, the exact amount they receive depends on the amount Tom and Jerry say in separate rooms. They receive the same amount if both end up saying the same number. Otherwise, If Tom ends up saying a lower number, he is given that amount plus a $2 bonus while Jerry gets the same amount with a $2 penalty for calling out a higher number.
THE DECISION(s)
At first, it is very simple to think that Tom and Jerry should both pick $100. However, given the history of their relationship; they do not want equal amounts, they want to “one-up” the other and receive the maximum payout.
As a result, Tom can predict that Jerry will pick $100, and therefore choose $99. Thus, the following payout will be the following
Tom: $99 + $2 bonus = $101
Jerry: $99 – $2 penalty = $97
Similarly, Jerry can predict that Tom will choose $99 and pick $98.
We can calculate all possible outcomes and arrange it nicely within a chart, and thus have the following:
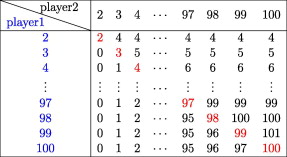
This thought process of predicting the other person’s number has a terminology in game theory also known as backward induction. At each stage of the game, you determine the optimal solution, then determine the next-to-last optimal solution and so on until eventually you hit the Nash Equilibrium; the minimum permissible amount where no player has a better optimal outcome given their choices. In this case, the Nash Equilibrium is $2 (see Figure 1).
Nash Equilibrium
In our case, the Nash Equilibrium does not really make sense as picking a higher number will have a higher chance of having a payout greater than $2. Let’s say the penalty amount is $40 for choosing the higher of the 2 numbers. This could result in a negative payout where either Tom or Jerry has to pay back the airlines instead. As a result, having a higher risk will make individuals more rational when making decisions. Thus, the chosen number will be closer to the Nash Equilibrium when more risk is involved.
Real-life application
The concepts shown has real-life applications that can be seen very often. For example, a person waiting in line for a brand new playstation. Given the limited amount of stock, let’s say if you wait in line before 6am you have a 50% chance of getting it. However, you can predict that if a person comes at 6:00am, you can come at 5:59am and have a higher chance. Another person can predict your prediction and end up coming even earlier. This will continue until you hit a Nash Equilibrium which is currently unknown to this problem.
Another applications involves companies who sell similar items fighting over on what the cost of their product should be. For example, gas stations in the same intersection deciding their gas price for the day. Both gas station can choose their price to be the lower of them both; however, this can result in increasingly greater losses in the process.
Conclusion
The traveler’s dilemma is an interesting problem that introduces one to many terminologies in game theory; which is the reason why I admire this problem.
Links
More about Traveler’s Dilemma: https://www.investopedia.com/articles/investing/111113/advanced-game-theory-strategies-decisionmaking.asp#toc-travelers-dilemma
Backward induction: https://www.investopedia.com/terms/b/backward-induction.asp
Video to watch for more information: https://www.youtube.com/watch?v=PQ7IN1bDa_I