People are making decisions all the time and in most cases, they want to make the “correct” decision that can maximize the benefit. However, the benefits of the choices are usually uncertain and no one will predict what exactly will happen in the future. Here is an example. Suppose you are catching a flight. Whether or not you can successfully catch it depends on multiple factors, such as the time that you get to the airport and the time taking to go through security. Moreover, the factors above also depend on some other factors such as how to get to the airport and the number of bags you have. These factors, however, influence the outcome in different ways. How to get to the airport only matters if you do not know when you get there while the number of bags still matters even if you know how long it takes to get through security since it also influences when you get to the airport. Now how will you make your decision? This post aims to introduce a new “network model” that can help with your decision-making under uncertain situations.
Introduction
To model the above-mentioned question, we will use the Bayesian network. It is a directed acyclic graph, in which the vertices
represent the different factors as random variables, and the edges represent the dependence relationships between them. Basically, if there exists an edge from V1 to V2, that indicates V1 and V2 are dependent and V1 causes V2. Bayesian networks are a type of probabilistic graphical model that uses Bayesian inference for probability computations, which aim to model conditional dependence, and therefore causation, by representing conditional dependence by edges in a directed graph. Through these relationships, one can efficiently conduct inference on the factors, which can be regarded as random variables, in the graph through the use of factors.
Modeling
Now we reconsider the above example and regard the factors as different variables:
• whether catch the flight or not, F
• time to get to the airport, T
• how long it takes to get through security, S
• how to get to the airport, M
• number of bags, N
Then we can construct a Bayesian Network over V = {F, T, S, M, N} as follows:
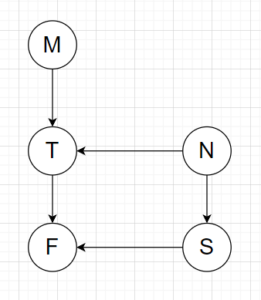
The network says the following:
• M causes T
• N causes T and S
• T and S cause F
Given the above graph, we want to find the probability of catching the flight given the method of transport, i.e., P(F|M). Suppose dom(F) = {yes, no}, dom(T) = {early, late} , dom(S) = {fast, slow},
dom(M) = {train, car}, and dom(N) = {0, 1, 2}, then the probability of catching the flight if we take the train is P(F = yes|M = train).
We first express the probability in terms of the joint distribution:
Then, we will be able to calculate P(F = yes|M = train) by substituting the probabilities into the formula. Note that it is easy to get the P(factor|its direct precessors) and we can use these probabilities to calculate the P(factor|its indirect precessors). Bayesian networks satisfy the local Markov property, which states that a node is conditionally independent of its non-descendants given its parents.
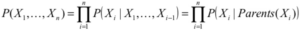
In real life, the target probability-related factors may have a very long distance from each other because most tasks will only directly use a small subset of the variables. And in this case, Bayesian Network will efficiently be used with variable elimination to reduce the computational cost.
Real-life application
Bayesian networks have already found their application in health outcomes research and in medical decision analysis such as health economic evaluation, health quality measurement, health outcomes monitoring, cost-effectiveness analysis, epidemiology, clinical research, medical decision-making, or public health. More generally, Bayesian networks can be used for both qualitative and quantitative modeling. Bayesian networks are able to deal with issues like data over-dispersion (by adding another node representing an additional error term to
the mean of every observation), the relationship between coefficients (representing the coefficients as nodes in the graph), missing data (each missing observation is represented as a node in the graph), measurement errors on covariates, measurement errors on observables, or further sources of complexity. In my opinion, it is a very useful tool for both practical use and abstract research in various fields with graph theory and graphic modeling.
Links
Introduction to Bayesian Networks