Introduction
Bitcoin is a digital currency which uses a decentralized ledger called blockchain to keep track of all the transactions. Instead of having a centralized authority (a centralized ledger) like bank to store transactions, the bitcoin is structured in peer-to-peer network where every peer is a node in the network. Due to the decentralized nature of bitcoin network, in order to ensure every node receives the new information, it uses the flooding algorithm to propagate information. It works as follows: “nodes will broadcast their desired information to each of their connected neighbours. Once received, the node’s neighbours will then in turn broadcast the newly received information to their neighbours, who will then broadcast it to their neighbours until eventually the information is received by all the peers in the network” [1].
Analysis
In the article that we will be discussing in this blog, the authors think the current implementation of flooding algorithm used by Bitcoin produces large number of redundant massages. They introduce a probabilistic flooding approach which reduces the duplicate information as well as ensuring the reliability and resilience. In the current implementation of information propagation in Bitcoin, the node will stop forwarding the same transactions or blocks to their neighbours if it already saw them before. Instead, the node will send an INV message to their neighbours. If a neighbour requires any of the transactions or blocks in the INV message, it needs to send back a GETDATA message to request for those, otherwise it can simply ignore the INV message, and no action is required. However, this produces a huge number of redundant messages. A node can receive multiple INV messages for same transaction from their neighbours since they do not know whether the node is missing any information.
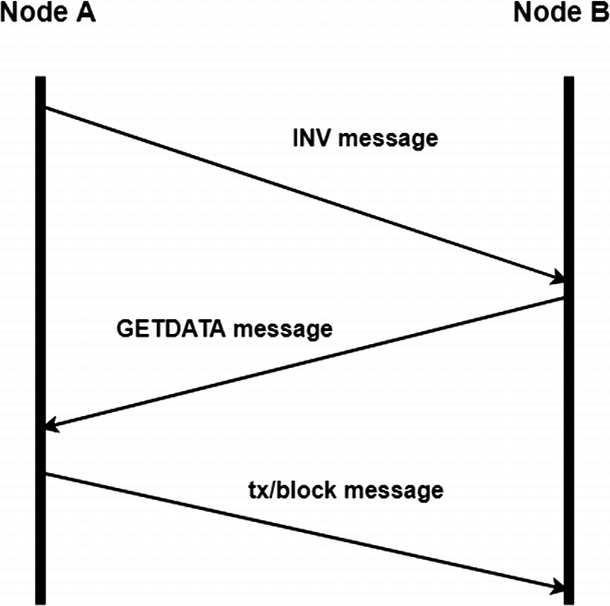
To reduce the redundant messages, the authors of An Efficient Peer-to-Peer Bitcoin Protocol with Probabilistic Flooding proposed a probabilistic flooding approach. “The idea of sending INV messages based on probability is centered around the fact that nodes in the Bitcoin network have a large variance in the number of connected neighbours.”[1]. In other words, some nodes are well-connected in the network, meaning they are connected with many neighbours, so there is a huge chance that they have already received INV message from their neighbours, the probability calculated for such nodes will be relatively low. On the other hand, some nodes only have a few neighbours, so it is possible that they might not received an INV message from their neighbours, the probability will be relatively high in this case. “The probability is calculated based on the number of INV messages sent to the neighbour and the number of GETDATA messages received in return from the neighbour.”[1].

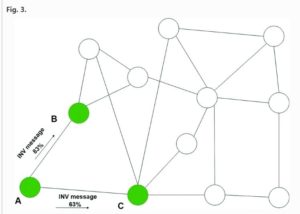
In the image above, the probability of node A sending INV message to node B is higher than sending to node C since C has more neighbours than B.
After testing the proposed probabilistic flooding approach, the result shows that their approach produced a 100% transaction commitment rate, means that every transaction is mined to a block. This ensures the reliability of system. The time taken for a transaction to be mined into a block is slightly less than current protocol. And lastly, there is a significant decrease in the number of redundant messages sent out compared to the current Bitcoin flooding algorithm.
Conclusion
The proposed probabilistic flooding approach for Bitcoin maintains the reliability of system by having 100% commitment rate of transactions. In addition, their approach reduces a significant number of redundant messages which makes it more efficient. This opens up more possibilities of improving the current flooding algorithm of Bitcoin in the future.
Reference
[1] Vu, H., Tewari, H. (2019). An Efficient Peer-to-Peer Bitcoin Protocol with Probabilistic Flooding. In: Miraz, M., Excell, P., Ware, A., Soomro, S., Ali, M. (eds) Emerging Technologies in Computing. iCETiC 2019. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 285. Springer, Cham. https://doi-org.myaccess.library.utoronto.ca/10.1007/978-3-030-23943-5_3