NBA 3 Pointers and Game Theory
Motivation
The NBA is filled with stats. To the point where during, after, and before every game, I’m just staring at stat sheets. Naturally, I’m going to look at the Game Theory of it all and see if I can apply more of what I learned to a topic I love.
NBA is pretty math driven, even though it may not seem that way. Coaches and analysts in an organization are always looking for the best way to optimize how they can win. For example, take high-percentage shots. Like a layup or a close 2-pointer. Or take a further shot, but it’s a three-pointer, so you’re well compensated for your increased risk. You likely don’t want to take a long two-pointer because it’s the same value as a layup but has increased risk. Similarly, you also don’t want to take a long 3. So why do Stephen Curry, Damian Lillard, Lebron James, and James Harden take them? Well, they make them. But why? Let’s find out.
Research
The research on this topic was done by Senthil Natarajan, an Electrical Engineering grad from Rice University out of Houston, TX. He frequently writes articles about the NBA and takes a mathematical approach. Others have also used his articles to write their own about them, such as students from Cornell University.
Analysis
Ok, why does Steph keep taking these long 3-pointers and making them? Yes, it’s because he’s good at it, but it’s not like he’s only good at 3s. He can score from anywhere, so why doesn’t he take layups, short 3s, or mid-range shots? Game Theory solves this mystery for us.
When I used to play basketball in High school, the coach broke down some of the three main ways you can defend the ball in the half-court. First, you can do a half-court press which is right up on the defence as soon as they cross half-court. This way, they have a harder time moving and taking threes, but they can blow past you and get a layup sometimes. You can be relaxed and guard closer to the rim, which has the opposite effect. It prevents higher percentage shots but leaves the three open. And there is the balanced approach which is a bit of both.
Here is a diagram of the payoff matrix and how it applies to game theory. This is very similar to what we learned in class.
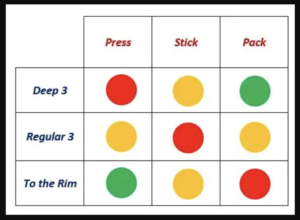
Given the three options, what does the favourable one depend on what the opponent does? Green is the opponent likely to close, red means they likely don’t, and yellow is in between.
So, how does this apply to regular players, and what does this have to do with long 3s? Natarajan also did the same kind of calculations on Stephen Curry and James Harden but this time, factoring in their actual statistics.
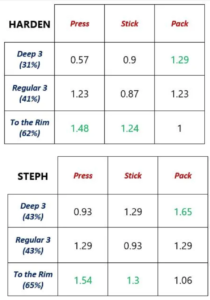
In the payoff matrices above, we can see that these two players are such great shooters that if you press, they’ll score so easily at the rim. The numbers are in units of points. For E.g. 1.54 is 1.54 points in that shot. If you pack (guard closer to the rim to prevent easier 2-pointers), they can easily hit a deep 3. And guess what? They’ll hit the deep three even more than a regular 3. So why wouldn’t they take that shot? You’re pretty much out of luck if you defend in between. That’s what makes these two so lethal, especially in their prime. No matter your strategy, they will do well, so how do we stop them?
Harden’s average payoffs are 1.09, 1.00, and 1.17, respectively. Stephen Curry’s is 1.25, 1.17, 1.33. The clear dominant strategy of the defence is to Stick because it yields a better result and to rarely pack because it yields the worst result (because they’re so good at deep 3s).
Ultimately the coaches will change play-by-play on what to do, but from a high-level math perspective, Game Theory provides us to answer the quick question of why superstars take deep 3s if they can score from pretty much anywhere.
Source
Natarajan, S. (2018, July 31). Nylon calculus: Game theory and the deep 3. FanSided. Retrieved November 7, 2022, from https://fansided.com/2018/07/31/nylon-calculus-game-theory-deep-3/
Networks. Game Theory in the NBA : Networks Course blog for INFO 2040/CS 2850/Econ 2040/SOC 2090. (n.d.). Retrieved November 7, 2022, from https://blogs.cornell.edu/info2040/2021/09/29/game-theory-in-the-nba/