Introduction
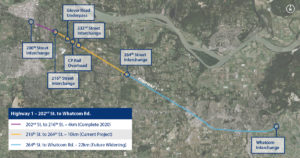
The Government of Canada, the Province of British Columbia, and the Township of Langley are all contributing to the widening of Highway 1, from the 216th Street to the 264th Street Interchanges. This decision is meant to help alleviate congestion and reduce transit times throughout the intersection, among other improvements.
According to the Daily Hive, once the construction is finished, Highway 1 will be increased by one lane in each direction, both of which will be reserved for HOV (High Occupancy Vehicles) and electric vehicles. Currently, the stretch of the highway being discussed has 2 lanes in each direction.
In order to understand how the widening of Highway 1 can make transportation better, we can use congestion game theory to determine how this change will affect vehicles along the highway.
Game Analysis
First, we need to set up the game model that we will use for this analysis.
Since the new lanes will not be available to all drivers, we will define our players as the drivers of electric vehicles using the highway. We do this because all players need to have the same strategies available, so they all need to be allowed on the new lanes.
Daily Hive states that approximately 90,000 vehicles use the given segment of Highway 1 each day. Since there are 2 directions, we have 45,000 vehicles for each one. Additionally, Vancouver Sun claims that zero emission vehicles make up 13% of all 2021 car sales in British Columbia. Since we have limited access to Langley’s transportation data, we can use this rough number as our estimate of the ratio of electric cars to gas cars that will be using Highway 1. Thus, we end up with 13% of 45,000 vehicles = 5,850 electric cars. Consequently, we are left with 39,150 drivers that can only stay within the old lanes. We will count them in our payoff values.
On this note, it is important to keep in mind throughout this paper that there are a lot more factors at play which are not being taken into consideration for this analysis. This filtering of data is a necessary step in the construction of our game model, but it can make the results somewhat less reliable.
Lastly, we have to define the payoffs for each situation. Since our goal is to measure the improvement from the new lanes, we can define our payoff functions as the number of cars in a lane, taken as a negative value. This way, once we have the results, we can calculate the difference between the number of cars in each lane while in equilibrium, from before and after the introduction of the new lane. This will tell us whether or not the traffic along the highway has had any significant improvements.
For the old lanes, we have, in addition to the players, 38150 cars that have to be divided between 2 lanes, so we can estimate around 19575 constant cars in each lane.
After our calculations, we now have the model for how to set up the game, which we will play twice. Initially, we will only use the 2 old lanes; then, we will include the new lane as an option.
INITIAL ROUND
Players: Drivers 1,2,…,11700;
Strategies:
- Use old lane 1, or
- Use old lane 2;
Payoff: negative number of cars in a lane
Equilibrium:
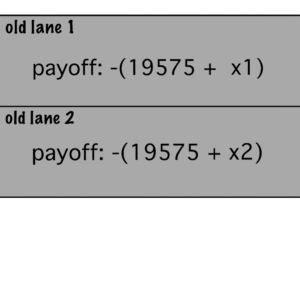
It is trivial to see that this game has an equilibrium when half the players choose old lane 1 and the rest use old lane 2. Thus, we can calculate this equilibrium to be at:
- old lane 1: -(19575 + 11700/2) = -25425
- old lane 2: -(19575 + 11700/2) = -25425
FINAL ROUND
Players: Drivers 1,2,…,11700;
Strategies:
- Use old lane 1, or
- Use old lane 2, or
- Use the new lane;
Payoff: negative number of cars in a lane
Equilibrium:
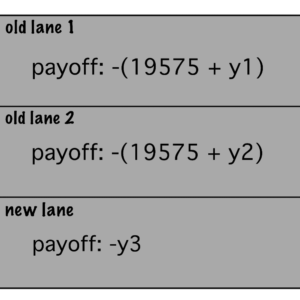
When all 11700 players choose to use the new lane and 0 players choose the old lanes, we have:
- old lane 1: -(19575 + 0) = -19575
- old lane 2: -(19575 + 0) = -19575
- new lane: -11700
This is also an equilibrium, since all players are getting the best strategy, so no one has the incentive to switch strategies.
Conclusion
In conclusion, we can use a simplified congestion game model to see how the new lanes can improve the traffic conditions along Highway 1. Despite our limited data, we were still able to gather enough information to construct a model that represents the improvements brought by this project. Using this model, we found that the addition of one lane in each direction of Highway 1 reduces the number of cars in each lane at equilibrium by 25425 – 19575 = 5850 vehicles.
Note: Since the new lane has no previous congestion value, we cannot define a measure of improvement.
This represents an improvement of 13% of the congestion along this stretch of Highway 1, which is a statistically significant amount. Therefore, we can see how useful Game Theory can be when applied to real-world issues.
References
https://news.gov.bc.ca/releases/2022TRAN0115-001693
https://dailyhive.com/vancouver/highway-1-216th-264th-widening-langley-construction