Game Theory and Reinforcement Learning in Werewolf Game

Currently, social deduction games have been popular among a lot of people, especially during the pandemic period. People find it enjoyable during the process of using logic and reasoning to uncover other players’ roles and meanwhile, can use communication and other means of bluffing to hide their own identities. Some good examples of such games would be Among Us, Werewolf game, Mafia, and so on. However, this kind of game is more complicated than the games that we covered in the lecture because players can communicate to influence the payoffs. This post aims to introduce modeling this kind of game with the game theory and then introduce how to find the “strategy” to play the game using reinforcement learning.

Introduction

Now we consider the specific social deduction game: the werewolf game. There are 2 parties in this game: Team Villager and Team Werewolf. Team Villager wins when all the werewolves are killed and Team Werewolf wins when the number of villagers is smaller than the number of werewolves. Team Villager may have players with special abilities such as a seer that can select a player to know if they are a werewolf every night.

This game is divided into 2 phases per round: day and night. During day time, players communicate with each other and gather information, then players votes to eliminate their suspected werewolf. During the night, special classes can use their abilities. For example, the werewolves can kill one player each night. Only werewolves are told who are werewolves whereas villagers have to guess.

Modeling

First of all, we can recall the game theory modeling defined in the lecture:

A game G is a tuple (P,S,O):

• P = set of Players
• S = a set of strategies for every player
• O = for every outcome (where every player is picking one strategy), a payoff for each player.

And for a general social deduction game, we can model it like this:

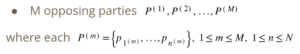
Basically, there are M parties and N players in total. Each set P represents a party, and it contains a set of players p_i. Every player p_i belongs to a party.

• The strategy S = A ∪ C where A is the set of game actions and C represents the communication between players.
• The payoff O corresponds to each status, which is related to the visibility of each player( whether the identity is visible to others) and the environment factor.

In the werewolf game, M = 2 since Team Villager P^(v) has villagers and other special players such as seer; Team Werewolf  P^(w) has werewolves. The game action includes voting for a player during the day and so on; the communication action may involve lying or pretending which can be very complicated, as well as the payoff.

Reinforcement Learning

In general, Reinforcement Learning is a method to learn how to choose actions given the environment in order to maximize a numerical payoff value. The learner needs to figure out which actions yield the maximum payoff by trying them out. Note that actions not only affect the immediate payoff but also all subsequent payoffs. 

The environment is shown as a state [s] to the agent. Then the agent can influence the environment by taking an action [a] and get the payoff or reward [r] for this [a, r] combination. The learner needs to repeat this process on each time step [t]. This can be shown in the following diagram: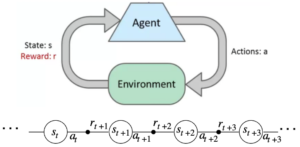

Moreover, among Reinforcement Learning methods, Q-learning is a model-free Reinforcement Learning algorithm to learn the value of an action in a particular state. It does not require a model of the environment (hence “model-free”), and it can handle problems with stochastic transitions and rewards without requiring adaptations. In our case, we can use Q-learning to estimate the value of rewards [r] for each action-state pair. Q-learning approximates the quality of an action taken for a state(which is the Q value). During the learning process, we repeatedly take action and update Q values. However, in this game, the environment and the size of state spaces will become too large for a traditional table representation of Q-learning. That is where the Deep Q Network comes in. Instead of using a table, we use a deep network to learn Q values. More specifically, each agent has one Q network to choose a target for voting. For Seer and Werewolves, each agent has two Q networks to choose targets for voting and using special functions. A diagram for a Q network is shown as follows: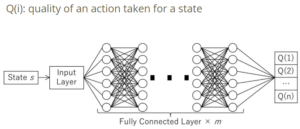

Outcomes

Here are the diagrams when we compare the Deep Q-Learning method with the other methods: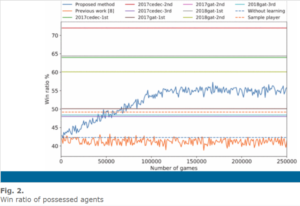

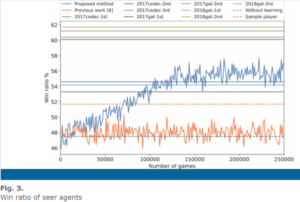
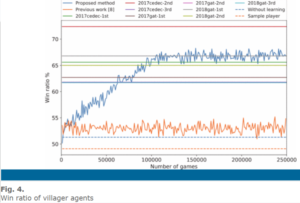
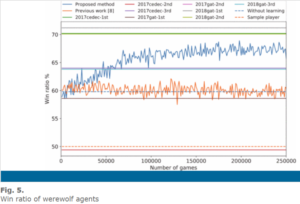
As is shown above, the Q-learning method which is the blue line is compared with another method without using the Q network, which is the orange one, as well as some other existing methods when playing as different kinds of agents. An interesting discovery is that, when playing against random agents, some AI agents have a relatively lower win rate while with contest agents it has a higher rate. This is because it also adopts the action patterns of the enemy players and the contest players usually have more complicated strategies.

As you can see QL method always has a relatively higher win rate, which means this method has better performance when building the game agents.

Conclusion

The reason why we use Reinforcement Learning instead of the traditional game theory methods similar to what have covered in class is that the state in this game depends on the communication and actions of all the players, so the state space is too large. Besides, single actions in this game might not be that meaningful because communication could be very complicated but still very essential in order to win the game. Furthermore, some players can lie and do something “meaningless for now” to prepare for future attacks. Therefore, it is difficult to evaluate states in the game and assign payoffs to actions. In contrast, Reinforcement Learning is proper for choosing a sequence of actions that lead to a strategy without modeling some payoff functions or finding heuristics. It can help AI agents to learn a strategy during the process of playing the game. This method can also be used to solve other similar social deduction games, which are pretty hard using pure game theory. Reinforcement Learning can train an AI agent to succeed in social deduction games in a relatively easier way.

References

Brandizzi N., Grossi D., & Iocchi Luca. (2021). RLupus Cooperation through emergent communication in The Werewolf social deduction game.

Hagiwara M., Moustafa A., & Ito T. (2019). Using q-learning and estimation of role in werewolf game. Proceedings of the Annual Conference of JSAI 33rd Annual Conference, 2019, pp. 2O5E303–2O5E303, The Japanese Society for Artificial Intelligence, 2019. 

Sutton, R. S. & Barto A. G. (1998). Reinforcement learning: An introduction. MIT press Cambridge. 

Wang, T., & Kaneko, T. (2018). Application of Deep Reinforcement Learning in Werewolf Game Agents. 2018 Conference on Technologies and Applications of Artificial Intelligence (TAAI), 28-33.