Clearly, water is one of the most crucial components to everyone’s existence on Earth. However over two billion people live in countries where water supply is inadequate, and approximately every 1 in 4 children will be in areas of extremely high water stress by 2040 (Unicef). As a result, in prevention and mitigation of a water crisis, many countries are conflicting over fresh water, this is even more-so the case in under-developed countries.
As we learned in class, game theory is the study of rational agents and their strategic decisions with payoffs. We saw some basic examples, such as deciding whether to study for an exam or prepare for a presentation, the prisoner’s dilemma, and matching pennies. However game theory is actually applicable to much more than this. As the field of game theory continues to evolve, it has been applied to some cases of resource conflict management. One such example of this, is the water resource conflict at the Teesta River, which is a body of water shared between both India and Bangladesh.
Agriculture in these two regions are heavily reliant on rain seasons, which occurs during the months of June to October. However during the dry seasons, a limited amount of crops such as seeds, can be grown without irrigation. India presides upstream of the Teesta river, and consequently, Bangladesh downstream of the river. Thus any work done upstream of this river by India will have detrimental effects, downstream of Bangladesh agriculture and livelihood.
In an effort to provide a theoretical solution, Mahmud and colleagues used a linear programming model to generate payoffs for each country depending on strategies of collaboration. Firstly, it should be noted that these payoffs developed in their model did not include any political or environmental monetary influences. Mahmud and colleagues formulated a mathematical equation to “maximize the net benefits of the power produced at the surface storage sites and of the irrigation water made available in the dry seasons of the year” (Mahmud et al, 2020). Pictured below are the parameters and constraints for their model.

Based on the following strategies and the model above, Mahmud and colleagues formulated the following payoff matrix:
India has three strategies which is as follows:
- Do nothing, and allow the river to naturally flow downstream.
- Use 70% of the waterflow and share 30% with Bangladesh during the dry season.
- Use 50% of the water flow and share 50% with Bangladesh during the dry season.
Bangladesh has two strategies which is as follows:
- Do nothing.
- Proceed with an irrigation project to improve agriculture during the dry season.
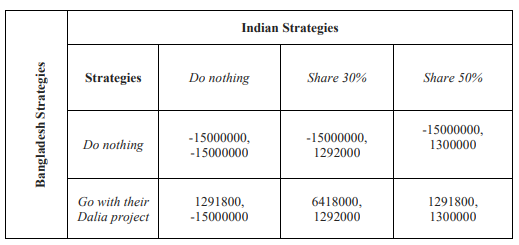
Notice that Bangladesh has a dominant strategy which is to always follow strategy 2, the irrigation project. Since Bangladesh will always follow strategy 2, it’s in India’s best interest to then use strategy 3, share 50% of the Teesta river, as this gives the highest payoff for them. Thus we see that there is Nash equilibrium at strategies (Irrigation Project, Share 50%), where Bangladesh gets a payoff of 1.29million cusec units of water, and India 1.3million cusec units of water.
To conclude, although some aspects of political and environmental influence were not involved in the calculation of the payoffs for each strategy for each player, this game theory application done by Mahmud and colleagues provides some insight on a possible solution for solving this water resource conflict.
Citations
Mahmud, F., Dulia, E. F., & Sen, A. (2020, December 7). A Case Study on Teesta Water Conflict: A Game Theory Approach. Retrieved November 17, 2022, from http://ieomsociety.org/harare2020/papers/154.pdf
Water scarcity. UNICEF. (n.d.). Retrieved November 16, 2022, from https://www.unicef.org/wash/water-scarcity