Game theory in poker introduction

When it comes to examples of zero sum games poker is one of the most commonly played zero sum games in the west. It would be infeasible to try and cover game theory for any state in poker so we will look at a heads up game of poker with 1 player having the most dominant possible hand preflop (Aces) and the opponent having the worst (2-7 off-suit). We will also only be looking at preflop play but rest assured even with this very narrow focus there will be a lot to cover. Because this blog post is not meant as a poker introduction but instead as an explanation to different thought processes the 2 players have during the game we will assume the reader has the most basic understanding of the rules of poker.1 of the first things that differentiate poker from the game theory examples learned in class is the idea of positioning. The game theory examples we went through in class have 2 players acting at the same time. However since 1 player acts after the other in poker this will factor into decision making. We will assume that 2-7 off suit is the small blind (and dealer since we are heads up) pre flop thus making aces the big blind. With it being the small blinds action they has 3 options, fold call or raise. If they chooses to raise they passes these same 3 options to the big blind.

Let’s look at the specific case of player 1 choosing to fold or call and player 2 then making the same 2 choices. Let’s look at each player’s perception of their odds.

Blinds: BB: 2, SB 1	Call	Fold
Call	0.37, 0.85	1, 0
Fold	0, 1	0, 1

The first thing you may notice is that while poker is a 0 sum game, the column call, call do not add up to 1. This is because this graph is not a representation of the actual odds both players have but instead what they perceive their odds to be. If both players knew each other’s hand exactly then all the squares would end up having a sum of 1 but because the players do not know, their perceived odds and actual odds differ. The next thing you may notice is that the column fold, fold has player 2 winning all the money. Because actions do not happen together, player 2 has the inherent advantage of knowing player 1’s actions and thus if player 1 folds player 2 will be the last player remaining to have a hand and thus win by default. Here we get a glimpse at the power of positioning. Now with this in mind, while player 1 (2-7) acts first preflop they actually act last post flop which is where a majority of the game is played. And this same advantage of acting is much more powerful in post flop play. Because both players understand that acting last post flop is an objective advantage, this means that player 1 can play a wider range of hands profitably and thus would be more willing to call with a wider range of hands as well as raise with a wider range of hands. 

In order for a call to be profitable in this situation player 1 would need to believe his hand is capable of winning some 25% of the chance for this to be a break even play (as they already has small blind committed into the pot).

Now obviously his odds are 37% so in a vacuum this player should always call. However this fails to take into consideration that player 2 has an action after player 1 acts, if player 1 calls the bet, therefore if player 2 decides to bet even 7 dollars after player 1 acts then this very quickly becomes an unprofitable play for player 1.

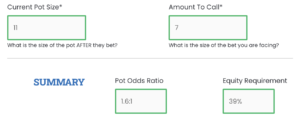From here we can quickly understand why it is best for player 1 to avoid this position all together and fold at his initial action. 

Let’s suppose however that player 1 is an absolute madlad and decides to raise. What does this say? This tells player 2 that player 1 highly values this hand (even though we know player 1’s hand is terrible, player 2 does not know that). So now player 2 has to reconsider where they are in the hand (the images below representing some of the hands player 2 may think player 1 has). Luckily for player 2, they don’t have much thinking to do because his hand is the best hand in the game preflop, calling and raising are both net profitable plays.

So player 2 never folds here (unless they have the habit of burning money). Player 2 now has an interesting choice to make, do they want to merely call the bet or do they want to further raise. Further raising is always profitable granted that player 1 calls the raise. Merely calling here gives player 2 the opportunity to under-represent their hand and thus player 1 playing with this information may call with weaker hands further down the line because they think player 2 is on average possessing a weaker hand. While this is good for player 2, it also gives player 1 the chance to improve on future streets and perhaps even improve to the winning hand, so there is always more risk involved in this play. Let’s suppose player 2 decides to raise. Lets now see an updated table of what the players may perceive their hand strengths to be.

Blinds: BB: 2, SB 1	Call	Fold
Call	0.25, 0.81	1, 0
Fold	0, 1	0, 1

As you can see, both players’ perception of their hand strength went down because both players played aggressively signaling strength. This is the main reason player 1 may choose to raise with an objectively weak hand to signal strength and potentially steal a pot of player 2 deems his odds to be lower than they actually are. We can continue this cycle of raise and raise until both players eventually call or one of the players choose to fold.

These above scenarios considered 2 players playing together for the first hand ever. What if the 2 players knows each others play styles? (Player 1 is aggressive and player 2 is more passive)

Assuming all the same actions as above (player 1 raises and then player 2 re-raises) both players perceptions of their own hand may look like this. Assuming both players have a good concept of poker ranges and both players play optimally, their assumptions about their hands reach close and closer to the expected value of call, call totalling 1.

Blinds: BB: 2, SB 1	Call	Fold
Call	0.15, 0.84	1, 0
Fold	0, 1	0, 1

Because player 2 knows player 1 is aggressive he knows that player 1 could be raising with a whole range of hands (not just their stronger holdings) and likewise since player 1 knows player 2 is more passive they know that for player 2 to raise their hand must be very strong. Thus player 1’s valuation of their hand dropped a lot while player 2’s only dropped by a little.

This shows just some of the decision making and game theory involved in a game like poker. Using merely 1 example hand at 1 stage in the game. Perhaps showing you the complexity of a game like poker and if nothing else showing you how game theory is involved.

Corrigan, Rory. “How You Should Think about Poker (but Probably Don’t).” Upswing Poker, 10 Dec. 2019, https://upswingpoker.com/gto-poker-game-theory-optimal-strategy/.