One of the most dangerous parts of living in a city, especially one with a large amount of both vehicle and pedestrian traffic is driving and crossing the roads. Due to this, we have many experts of the city carefully, and after much deliberation with each other come up with road laws that are implemented by our political systems to ensure our safety for everyone including; drivers, pedestrians, and cyclists. However, do these rules really help us if the people in the area deviate from them, because it may not be the most natural strategy? This is where game theory comes in and its analysis will give us Nash equilibria that can be compared with the road rules and what people actually do at crossings. This will help us figure out if game theory is powerful enough to predict real world situations and we may be able to use the findings to implement rules that most people will actually be inclined to follow, which in turn will help us create a safer community to live in.
This is exactly what Torkel Bjornskau studied, when focusing on the road crossings (zebra-crossings) and give-way rules of Norway. The current formal rules for Norway road crossings is that both cyclists and pedestrians can share the sidewalk, and by extension share the zebra-crossings. However, drivers must yield to crossing pedestrians, but cyclists must yield for the driver, unless the cyclist dismounts from their bike and walks across the crossing. We can model the interaction between the driver and cyclist at the crossing by assigning the cyclist 3 strategies:
- A: Cyclist gives way to driver
- B: Cyclist continues to cycle over zebra-crossing
- C: Cyclist dismounts from their bike and walks, making driver give way
Similarly the driver has 2 strategies:
- X: Continue to drive forward
- Y: Give way to the cyclist
According to the crossing rules of Norway the two set of strategies that align with the rules themselves is {A, X} or {C, Y}. However, after observations by Bjornskau and his team on three zebra-crossings it turned out that most cyclist-driver interaction did not follow the formal rules of strategies AX or CY. Instead the most common interaction was for the cyclist to continue over the crossing and the driver to yield for the cyclist even if they don’t really need to, according to the rules (strategy {B, Y}). The next step is to see if after applying game theory to this interaction do we still get {B, Y} as a equilibrium and a natural strategy.
We will need to make slight modifications to the game theory model from class. This traditional model emphasizes the themes of rationality and simultaneity between the players. However, when it comes to modelling traffic interactions, quick decisions have to be made so full rationality might not be fully accurate, also we have the fact that traffic interaction is constantly repeating. So, we need a more dynamic game theory model that can also cover that fact the same game is played multiple times with different players. Hence, Bjornskau models his “Zebra Crossing Game” after the “Leader” game theory games found in previous studies of game theory’s relation to traffic interactions. Here instead of our payoff being an arbitrary value in a matrix, we have payoffs as a ranking of the different possible outcomes. So since the cyclist has 3 strategies and driver has 2 we have a total of 3 x 2 = 6 outcomes. Just like usual we want to maximize payoff, so the outcome a player wants the most we give it payoff 6 and the outcome player wants the least we give that a payoff of one.
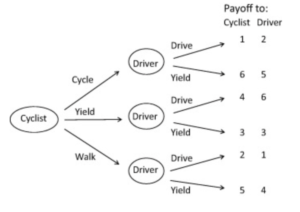
The above figure show the payoffs for the Zebra Crossing Game. As you can see the cyclist best scenario would be a payoff of 6 when they continue to cycle and driver yields. For the diver the best payoff is if cyclist yields and driver continues forward. On the other end of the spectrum (1 and 2) both for cyclist and driver these would be the collision scenarios, but 1 and 2 are swapped for the players depending on who will receive greater compensation. For example, a collision where cyclist walks is better than collision when cyclist cycles for the cyclist because when they walk they are actually obeying the rules and will probably receive more compensation. Also for both players giving way to the other player to proceed is better than both giving way since if both gave way then the game would need to be replayed and no progress would be made. Similarly all other scenarios and the driver’s and cyclist’s respective payoffs are modelled by the tree in the above figure.
Now, Bjornskau did an analysis of the game to figure out the Nash equilibria of the game (similar to class, equilibrium is a pair of strategies where no player has the incentive to switch). Notice that in the modelled game that one of the formal rule strategies Walk/Yield (CY, [5,4]) is not an equilibrium. The equilibria of the game are Yield/Drive (AX, [4,6]) and Cycle/Yield (BY, [6,5]). Bjornskau reasons that if the cyclist arrives at the crossing according to the rules they either must give way and let the driver go [4,6] or they must dismount and walk and driver will yield [5,4]. Now since this model of game theory we don’t have strong emphasis on simultaneity, we can say cyclist will have first move. So out of the 2 formal rule strategies since 5>4 the cyclist will choose to dismount and walk (strategy CY), this will mean for the driver to maximize their payoff, they must yield for the cyclist. However, now given that the driver will yield, the cyclist will realize that it’s better to just cycle across the zebra-crossing as that will increase both the cyclist’s and driver’s payoff (strategy BY, 5 to 6 for cyclist and 4 to 5 for driver). This will be a stable pair of strategies as strategy BY is an equilibrium in the game.
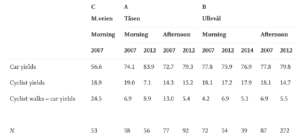
The game theoretic result of strategy {B, Y}, where the cyclist continues to cycle across and the driver giving way to the cyclist is exactly the majority result Bjornskau and his team found when observing 3 zebra-crossings in Norway, as mentioned above. In the above figure we see our game theoretic result is close to the real world observations despite it not adhering to the formal crossing rules that were established. We see that even though the cyclist needs to give way to driver when deciding not to dismount, the real world results from all 3 crossing shows the driver is yielding the majority of the time and letting the cyclist cross. It is important to note that while all 3 crossings show car yielding as majority, the reason why crossing C’s car yield is much lower than the other 2 crossings is because, the location at C according to Bjornskau is a very urban area with a lot of slower moving pedestrians, which means cyclists move in that area much slower so it actually is not a big deal to dismount and walk across the zebra-crossing at location C (M.veien crossing).
Here, game theory was used to predict very accurately the traffic interactions at road crossings in the real world, despite the result being different than the formal crossing rules in place. With his game theory analysis, Bjornskau in 2001, despite the rule being for cyclist to yield for drivers, he accurately predicted that in a few years the drivers will yield for cyclists which is the real world outcome that occurs majority of the time. This shows game theory is very helpful in modelling and predicting traffic interactions, and with this understanding we can also use better logic to implement better traffic rules and other resources to ensure the greater safety for the whole population.
Source:
Bjornskau, T. (2017). The Zebra Crossing Game – Using game theory to explain a discrepancy between road user behaviour and traffic rules. Safety Science, 92, 298–301. https://doi.org/10.1016/j.ssci.2015.10.007
Used the UTSC library’s link to access the article: https://librarysearch.library.utoronto.ca/permalink/01UTORONTO_INST/fedca1/cdi_proquest_miscellaneous_1864572154