Deadlock Dilemma

Similar to the Prisoners Dilemma, there is another commonly scenario known as “Deadlock”. First created by William Pounderstone, this social dilemma while similar to the commonly known Prisoner Dilemma adds on a new concept that changes it from being the same scenario.

Description

In this social dilemma, there are 2 players. Each one has an option to either cooperate or defect. If there is a “deadlock” i.e. (both players choose the same option) if that same action is to cooperate, both players get awarded a payoff of 1. If the same action chosen by both players is defect, then each player is rewarded a payoff of 3. If either player chooses cooperate, while the other chooses defect, the player who chose defect will be awarded a payoff of 3 while the player who chose cooperate will receive nothing.

Analysis

We can start by making this into a payoff matrix. Exactly with the information mentioned in the description we can plot this as follows:

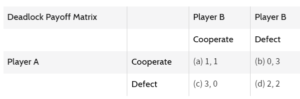
The main way this defects from the commonly known “Prisoners Dilemma” is that in that scenario the optimal decision was for both parties to cooperate. This framing of the situation is completely identical in the sense that players have options of either cooperating of defecting but in this one the dominant strategy is actually for both players to defect (as you can see in the payoff matrix, it is always optimal for both players to choose “defect”).

While this might be conflicting at first why these extremely similar situations contain polar opposite optimal solutions, it can be better explained by forming the idea of “deadlock” into a scenario. Consider if Player A was a country and Player B was a counter-part country that had conflicts with Player A. Both countries are threatening war with nuclear warheads. The agreement comes out to be either both parties cooperate and remove their nuclear warheads or defect. In this scenario, defect refers to agreeing to remove their nuclear warheads and still secretly retaining their nuclear warheads. When phrased like this, it can easily be seen that the optimal solution for a country, while quite unethical would be to lie about removing their nuclear warheads while retaining their own. By doing this, there are two possible outcomes, the other country (Player B) genuinely removes their warheads giving Player A a huge payoff (advantage) in comparison to Player B. Or, Player B also reneges and lies about removing their warheads, while retaining their own and in which case we are back at a neutral standoff.

 

Conclusion

I like the whole Deadlock situation because it corresponds to such a popular known dilemma (The Prisoners Dilemma) while maintaining a very similar situation with the exact same options and shows that the optimal solution is always based on the payoff matrix. The two parties were given the exact same two choices as the Prisoners Dilemma but a completely opposite dominant strategy was used here, and there are various applications where this will be the case (The nuke one mentioned above is just one of the most popular).

 

Resources

Deadlock (game theory). Wikiwand. (n.d.). Retrieved November 19, 2022, from https://www.wikiwand.com/en/Deadlock_(game_theory)

Picardo, E. (2022, July 13). How game theory strategy improves decision making. Investopedia. Retrieved November 19, 2022, from https://www.investopedia.com/articles/investing/111113/advanced-game-theory-strategies-decisionmaking.asp

Shor, M. (n.d.). Dictionary :: Games. Deadlock – Game Theory .net. Retrieved November 19, 2022, from https://www.gametheory.net/dictionary/Games/Deadlock.html