The Prisoners Dilemma & Hockey Standings

Often times in professional sports with two competing teams, “regulation time” is not satisfactory for determining a victorious team. This occurs when both sports teams are tied by the end of the game’s scheduled duration. There are several ways to handle such an outcome – some sports deem these as ties, and other sports add additional overtime periods that keep going until a period ends with one team ahead of the other team.

In 2004, the NHL commissioner Gary Bettman controversially decided to take something of a hybrid approach. Beginning with the 2004-05 NHL season, if a hockey game didn’t have a conclusive winner after five minutes of overtime, a “shoot-out” would determine the winner of the game. Regardless, in both of these outcomes, there would be a conclusive winner. This meant that regulation wins would be weighted the same as overtime/shootout wins, but with Bettman’s new rule, teams that lose in overtime/shootouts will still gain something in the overall league standings, while teams that lose in regulation gained nothing.

Context

In the NHL, the standings are the main measure for a team’s success. Only the best teams from the standings would be considered in the playoffs. A team’s position on the standings considered how many “points” they had. Teams with more points had higher positions on the standings than teams with less points.

Prior to Bettman’s rule change, each win gave a team 2 points, each loss gave a team 0 points, and ties gave 1 point each to both teams involved. With Bettman’s new rules, a win (both in regulation and in overtime/shootout) gave teams 2 points, losses in regulation gave teams 0 points, and losses in overtime/shootout gave the losing team 1 point.

This change was widely controversial among NHL fans when the rule was implemented. Some fans felt that teams that lost, regardless of whether it was in regulation, should not have been rewarded. Other fans were concerned that this would lead some teams to conspire together so that games will be determined in overtime, allowing for a greater benefit for both teams, while coming at the cost of the integrity of the game. In Xavier Weisender’s article, he considers the latter concern, and uses game theory to analyze the validity and potential impact of this concern.

Analysis

Weisender considers the situation where there are two different players in the game (representing distinct hockey teams playing against each other). In this situation, there are 5 minutes left in regulation time, and the game is tied. Here, Weisender checks if there is any truth in the idea that conspiring together is mutually beneficial to both teams. The payoff matrix below describes Weisender’s estimate for the average amount of points that would be received by each team for the given situation. Note that Player 1’s choices are represented along the X axis and Player 2’s choices are represented along the Y axis. If a team decides to wait for overtime, then they will not try to score on offense, and will focus on defense. If a team tries to win in regulation, then they will try to win the game in regulation, but if they cannot do this, they will try to win in overtime. The payoff values in the matrix attempt to represent a rough estimate that considers all of the mentioned factors to determine how much points these outcomes would generate on average.

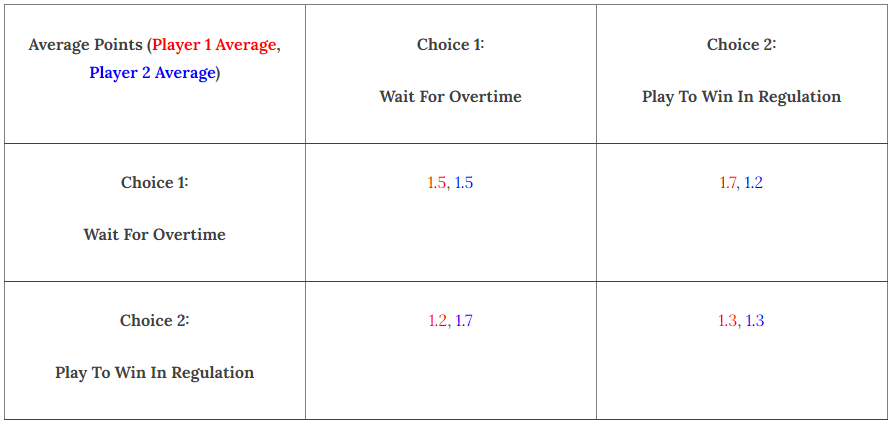
It is important to note that this game works under the assumption that both teams are equally competitive if they give the same amount of effort. The NHL, especially compared to other sports leagues, is known to be a league with a high competitive balance, and also that the assumption works knowing that both teams have evenly matched up for most of the game (since the game is assumed to be tied). This assumption allows us to state that if both teams wait for overtime or play to win in regulation, they will have the same average points gained.

In this case, the Nash equilibrium occurs when both teams play to win in regulation. This is because if it is known that one team plays to win in regulation, it is always optimal based on the point values for the other team to play to win in regulation to maximize the points they get.

Conclusion

In this case, we can see that the situation where both teams play to win in overtime describes the event for the Nash equilibrium. This means that we can describe this as a strictly dominant strategy for both players. However, we can see that this situation is strictly inferior for both teams than if they were just to mutually agree to wait until overtime, assuming both teams hold up their end of the deal. This explains the concerns that some fans had about this rule change, in that it would provide a benefit for both teams while compromising the integrity of the game. However, in viewing it in a similar perspective to the Prisoner’s Dilemma, we can see that this potential in gained points is largely lost because both teams would rationally decide to win in regulation, inevitably leading to the Nash’s equilibrium.

Citations

Xavier Weisenreder (n.d.). The Bettman Point and the Prisoner’s Dilemma. Georgetown Sports Analysis. Retrieved November 23, 2022, from https://georgetownsportsanalysis.wordpress.com/2014/01/02/the-bettman-point-and-the-prisoners-dilemma/