In the past few years, there has been intense competition and rapid innovation between Tesla, Google, and Uber to see who can create the first practical self-driving car. Each company has extensive applications for the use of self-driving cars. To name a few, Google could use self-driving cars for expanding Google maps street view, Uber could have self-driving cars to pick up passengers and Tesla could provide consumers with new autonomous car features to improve their lives.
But what technology and algorithms are required to create an autonomous self-driving car? Excitingly, we already know one of those theories required to design a self-driving car–Game Theory!
(The following examples and algorithm are from the research article “Game-Theoretic Lane-Changing Decision Making and Payoff Learning for Autonomous Vehicles”, Lopez 2022)
When driving on the road, a self-driving car is required to make decisions on whether or not it should change lanes or continue in its current lane. As discussed in the research article, a self-driving car (sd car for short) has two objectives:
1) to maintain a safe distance from other cars, and
2) to keep a steady speed.
However, in order to meet these goals the sd car must consider the fact that the other cars around it also wish to accomplish those two goals. On the road there are multiple other cars also looking to optimize their objectives such as in Image 1. We would need to find a Nash Equilibrium for N players which is very computationally intensive. Therefore, the sd car, instead computes multiple 2 player Nash Equilibriums between itself and the other cars on the road. Then it analyzes which of the payoffs from each of the pairs is maximal and then chooses that action to take.
Consider the following situation from player E’s (sd car) point of view:
Image 1: Players E, LB and RB on the highway. (Source: Figure 2, Lopez 2022)
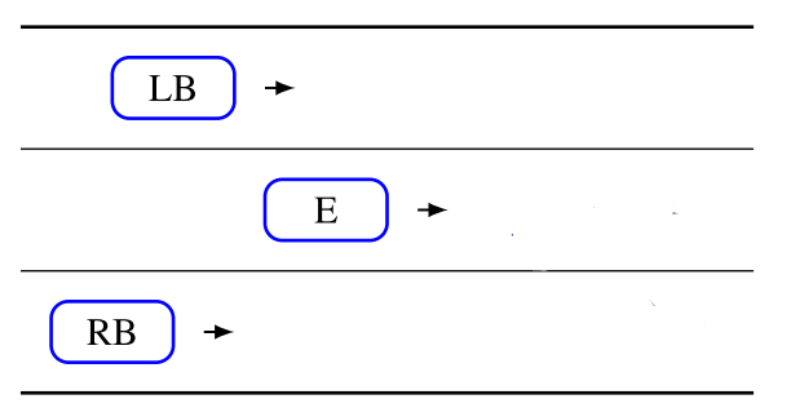
Player E has the following 3 strategies:
- Keep going in their current lane
- Switch to the right lane
- Switch to the left lane
Players LB and RB have 2 strategies:
- Reduce their current speed and let E switch lanes
- Keep going at their current speed (which prevents player E from changing lanes)
Note that in the research article, they determined all the payoffs for each combination of strategies using machine learning. If you wish to learn more about how they determined each payoff then you can continue reading in the article linked below at the end of this blog post.
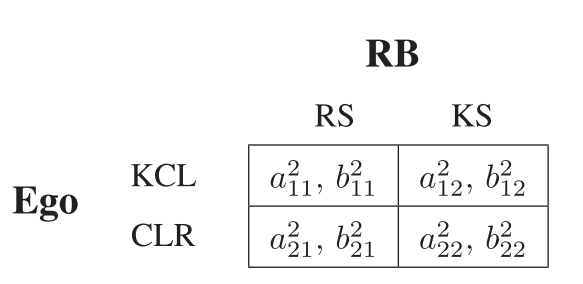
Consider the following scenario where player E is on the highway and to their back left is another player LB and to their back right is player RB. In order to find their best move, player E must play two games simultaneously with LB and RB to decide what is the best strategy to take (see images 2 and 3 below). If the Nash equilibrium from both of the two games are to keep its current lane, then player E will keep its current lane. But if the Nash Equilibrium from one of the games allows for player E to change lanes but other does not, then Player E will obviously choose to change lanes in that direction. If both of the Nash Equilibriums allow player E to switch lanes, then player E will see which of the two lane switches has the highest payoff and make the decision accordingly. However, the decision taken by player E may be optimal at this period in time but in a matter of a few seconds player LB or RB could decide to accelerate or perform irrational actions. Therefore, player E must constantly replay the same game every few milliseconds to determine the safest and most optimal decision at any given point in time.
Image 2: Payoff Matrix for players E and LB. (Source: Figure 3, Lopez 2022)
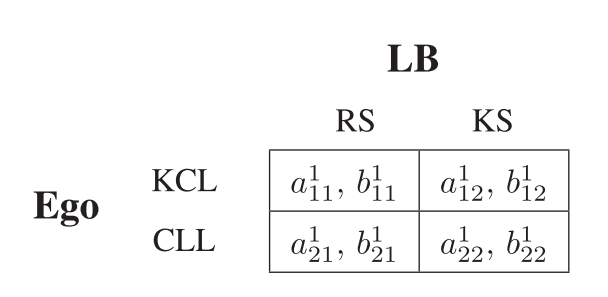
Image 3: Payoff Matrix for players E and RB. (Source: Figure 4, Lopez 2022)
Sources:
Lopez Mejia, V. G., Lewis, F., Liu, M., Wan, Y., Nageshrao, S., & Filev, D. (2022). Game-Theoretic Lane-Changing Decision Making and Payoff Learning for Autonomous Vehicles. IEEE Transactions on Vehicular Technology, 71(4), 1–1. https://doi.org/10.1109/TVT.2022.3148972