Why do breakaway strategies fail in racing? 🏍️

Introduction

When it comes to racing, and especially cycling, there are two types of strategies; peloton and breakaway. The peloton refers to the center of the pack – a large group of cyclists that stay relatively close together to benefit from a slipstream. There are often cyclists that attack at the beginning of the race forming a breakaway from the peloton. This breakaway strategy has been shown to fail with some experts saying that it is not the optimal strategy 9 times out of 10. And the reason? Physics and game theory.

As a fan of MotoGP and a motorcyclist, I always wondered how big of a factor slipstreams are in long races and why racers tend to stay in groups. One’s intuition to always be ahead and stay ahead may not be a very good strategy. I am surprised to find out that part of it has to do with game theory. In this post we will look at how these strategies are shaped by game theory in cycling and in autonomous racing.

Cycling

In an article titled “Can Game Theory explain bike racing?” by Alex Malone, he goes on to describe the similarities between the Prisoner’s Dilemma and bike racing (Cyclist, 2015).

I will illustrate this with the following example: there are two riders, rider A and rider B. Both riders can choose between two strategies; peloton and breakaway. The payout for each strategy works as follows: if both rider A and rider B both choose peloton, then a Nash equilibrium is reached as neither player can slipstream off of each other and if either player plays breakaway, the other player will be able to slipstream. If both players pick breakaway, then both players are incentivized to play peloton to slipstream.

This simple principle has shaped the strategies of cyclists. Funnily enough, because of this, races do not optimize the fastest average speed of the group. Riders would much rather slow down to be behind the leader, than to stay ahead and use a lot of energy.

Autonomous Racing

A research paper titled “A Non-Cooperative Game Approach to Autonomous Racing” by Alexander Liniger and John Lygeros analyzes the game theory decisions needed for autonomous racing. This forms the perfect basis for discussion as autonomous vehicles need a systematic method to make decisions – what better way than to apply game theory to quantify a payout for these decisions.

The paper defines the payout as the distance traveled – in our case it is measured by laps and fractional laps – up to 10 laps.

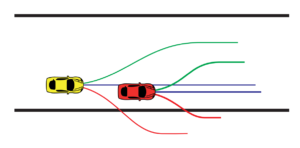
One of the decisions analyzed was when racers are given 3 routes to take, each colored differently. The payout is as follows where A chooses the row and B chooses the column (top to bottom, left to right). Car B is the yellow car, and car A is the red car.

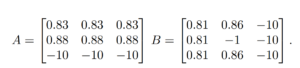
We can see from this payout matrix that it assumes that it costs some lap distance to swerve to a different lane position. There is also a minor benefit for the red car to block the yellow car. Veering off-course gives the worst payout of -10 laps. Very interesting so far, but the paper also analyzed an additional strategy – the blocking game.

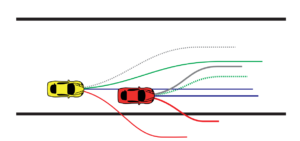
The blocking game refers to a front racer attempting to block the racers behind to prevent overtaking by swerving in their way. In this scenario, the yellow car can pass with the green line. The red car can block it by going the dotted green path. The dotted gray path allows the yellow car to pass unless red plays the gray path. We still have player A as the red car and player B as the yellow car.

The addition of + 0.5 represents the bonus each car has if they are able to successfully pass or block the other car.

The paper then analyzes different equilibria of both the blocking game and the cooperative game. In the cooperative game, where both players are trying to maximize their payouts regardless of whether they finish first or second. In the cooperative game, one such equilibrium is (1, 2) where car A goes straight and car B goes up top. Car A cannot have a better move, and B cannot either as going straight would collide with A and swerving down would go off-road.

It was found that in the blocking game, there was no Nash equilibrium. It was found that “… for (i, j) to be a Nash equilibrium of the blocking game, it also needs to be a Nash equilibrium of the cooperative game.” (Liniger & Lygeros, 2019). Some other very interesting observations were made, such as how if the additional bonus for passing was removed, then it becomes identical to the cooperative game.

Conclusion

It is incredible to see how these estimates are made to model real life scenarios. The blocking position in the autonomous racing paper outlined how important the bonus payout is for passing another car. Without a bonus, it becomes cooperative. The value must be large enough to properly model real life payouts. From reading these articles, I have realized that there are plentiful scenarios to apply game theory in life, however the approximation of the payouts, as well as the assumptions that must be made, are a major challenge.

References

Cyclist. (2015, February 25). Can game theory explain bike racing? Cyclist Australia/NZ ‘ The thrill of the ride. Retrieved November 24, 2022, from https://cyclist.com.au/can-game-theory-explain-bike-racing/

Liniger, A., & Lygeros, J. (2019, January 10). A non-cooperative game approach to autonomous racing. arXiv.org. Retrieved November 24, 2022, from https://arxiv.org/abs/1712.03913