Evolutionary Game Theory and Algorithms

Introduction – definition of Evolutionary Game Theory

First, let’s take a high-level overview of what Evolutionary Game Theory is. Based on our understanding of classic game theory, we give Evolutionary Game Theory a definition similar to the classic one. The difference about Evolutionary game theory is that it involves the dynamics of the strategy changes affected in the population. In one word, the players are playing independently and simultaneously in a classic game theory and the strategy they choose is static without changing, while the players are influenced by each other’s strategies and will change their own strategies accordingly in evolutionary game theory.

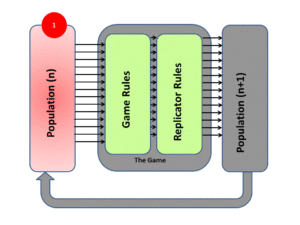
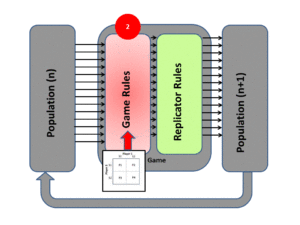
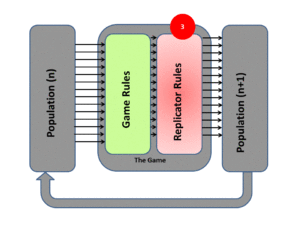
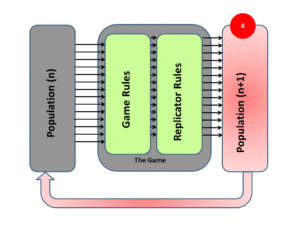
Approaches of Evolutionary Game Theory

The Evolution of game theory was first developed by biologists when studying the evolving population of social animals. Unlike the assumption we make that players are rational when discussing classic game theory, the players are not required to be rational in evolutionary game theory since the best strategy is selected naturally for us. In general, there are two main approaches to evolutionary game theory:

1. Evolutionary stable strategies (ESS)

The ESS describes a situation when the whole public keep an adaption of one strategy and any new other strategies will vanish. Hence, a problem raised when we connect this to how the evolutionary game theory first developed. According to Darwin’s natural selection, the individuals only choose the strategies best for themselves (i.e., increase their own payoffs in our understanding of classic game theory). However, there do exist the possibility of cooperation where people can negotiate and choose the payoff best for both of them (e.g., both students choose to prepare for Presentation in our Week8 lecture example).

2. Analysis of frequency of different strategies

Take an example of cooperation and defection. From the short-term payoff matrix, we can tell that it is always better to defect from cooperation. However, after a number of repetitions, players are more into cooperation, which will provide them a stable optimal strategy.

To come up with an optimal strategy, we have two common algorithms similar to our pure Nash Equlibria and mixed-strategy:

• Pure Tit-for-tat
  • Starting with cooperation of Player1;
  • If Player2 cooperates, then Player1 will cooperate;
  • If Player2 defects, then Player1 will defect.

It is shown that cooperation will be adopted when players are using Tit-for-tat strategy.

• Generous Tit-for-tat (with randomness)
  • Starting with cooperation of Player1;
  • If Player2 cooperates, then Player1 will cooperate;
  • If Player2 defects with some random probability, there is still a chance for Player1 to continue cooperation.

The generous tit-for-tat strategy is usually adopted when we are not sure about the trustworthy of cooperators.

Applications of Evolutionary Game Theory

When a new idea comes up, the majority of the public follows the bandwagon effect. Accordingly, the evolutionary state of the population became stable when most of the population adapt this strategy. Even though there might be some new opinions, they will be ignored and finally disappeared among the advocations of the mainstream view.

Thus, in any field insisting on the evolutionary stable strategy, a strategy can only be valuable if it insists and maintains stable after the adaption process (like “cooperation” in our above examples), which is the period when the audience are affected by the mainstream view and will modify their own strategies accordingly.

Reference

https://en.wikipedia.org/wiki/Evolutionary_game_theory

Ozkan-Canbolat, E., Beraha, A., & Bas, A. (2016). Application of Evolutionary Game Theory to Strategic Innovation. Procedia – Social and Behavioral Sciences, 235, 685–693. https://doi.org/10.1016/j.sbspro.2016.11.069