Introduction
Quantitative risk analysis is a fundamental concept in computer security and is also one of the first topics introduced in CSCD27 (Computer and Network Security). To summarize, it involves calculating risk exposure for potential threats to a system, by a simple formula: (probability * impact). This allows the risk “manager” to prioritize certain threats over others based on their risk exposure score. One main component lacking from this simplistic approach is modelling cost effective defense mechanisms against threats. That is where game theory can come into play. In this blog, I will be summarizing a research paper that models threats and their defence mechanisms using a 2 player game strategy.
Background
Game Trees
In class we learned some basic definitions of game theory: Payoff, Payoff matrices, Game (P – players participating, S – strategies O – outcomes). In “simple” games, a payoff matrix can pretty much summarize all the possible game states for us. However, in complex games such as checkers and chess, where the next move by a player is determined by “thinking ahead”/predicting their opponent’s next play, a structure such as a game tree comes in really handy. A game tree is another method of visualizing 2 player games and payoffs. In essence, one level of the tree is controlled by a player, the next by its opponent and so on. This allows us to simulate a turn-taking 2 player game.
Aside: For simplicity, I am omitting many details about game trees, their formulization (search space/algorithms), and consequences. If you are curious about adversarial game AI’s , game tree search (minimax), etc. , I highly recommend taking CSC384/D84.
Information Security Model
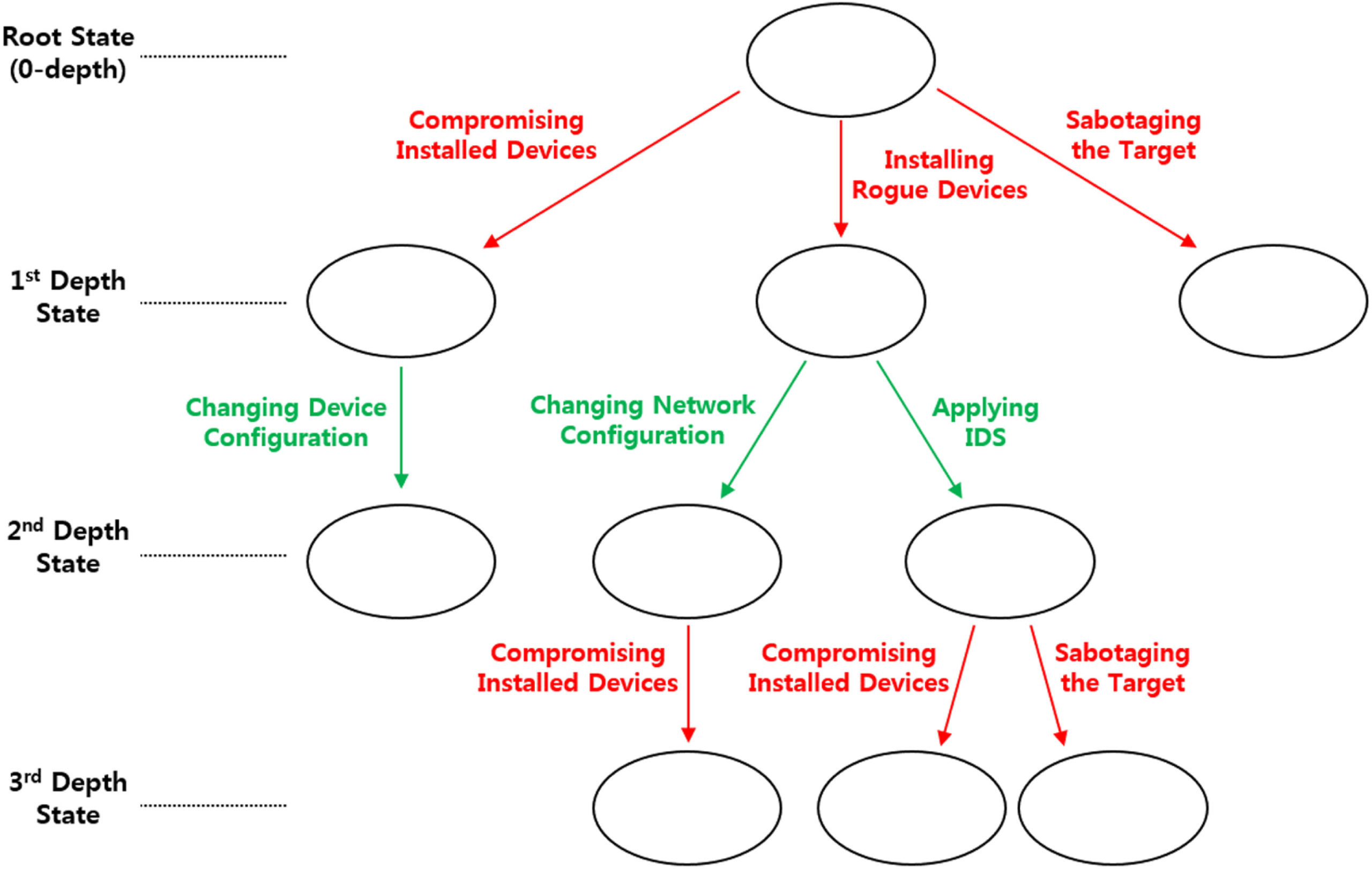
Quantifying security vulnerabilities
As mentioned in the introduction, a simple risk exposure formula does not account for the possible mitigations to a threat and their effectiveness. Game trees are a tool which can allow us to “traverse” various possible paths, accounting for the actions taken by a hacker and security admins together and come up with a outcome.


![]()
Using the game tree model and the payoffs with real data
After defining the payoffs, the impact, etc. the article goes through a scenario of a DoS attack on a software system, modelling the possible mitigations against it using game trees.
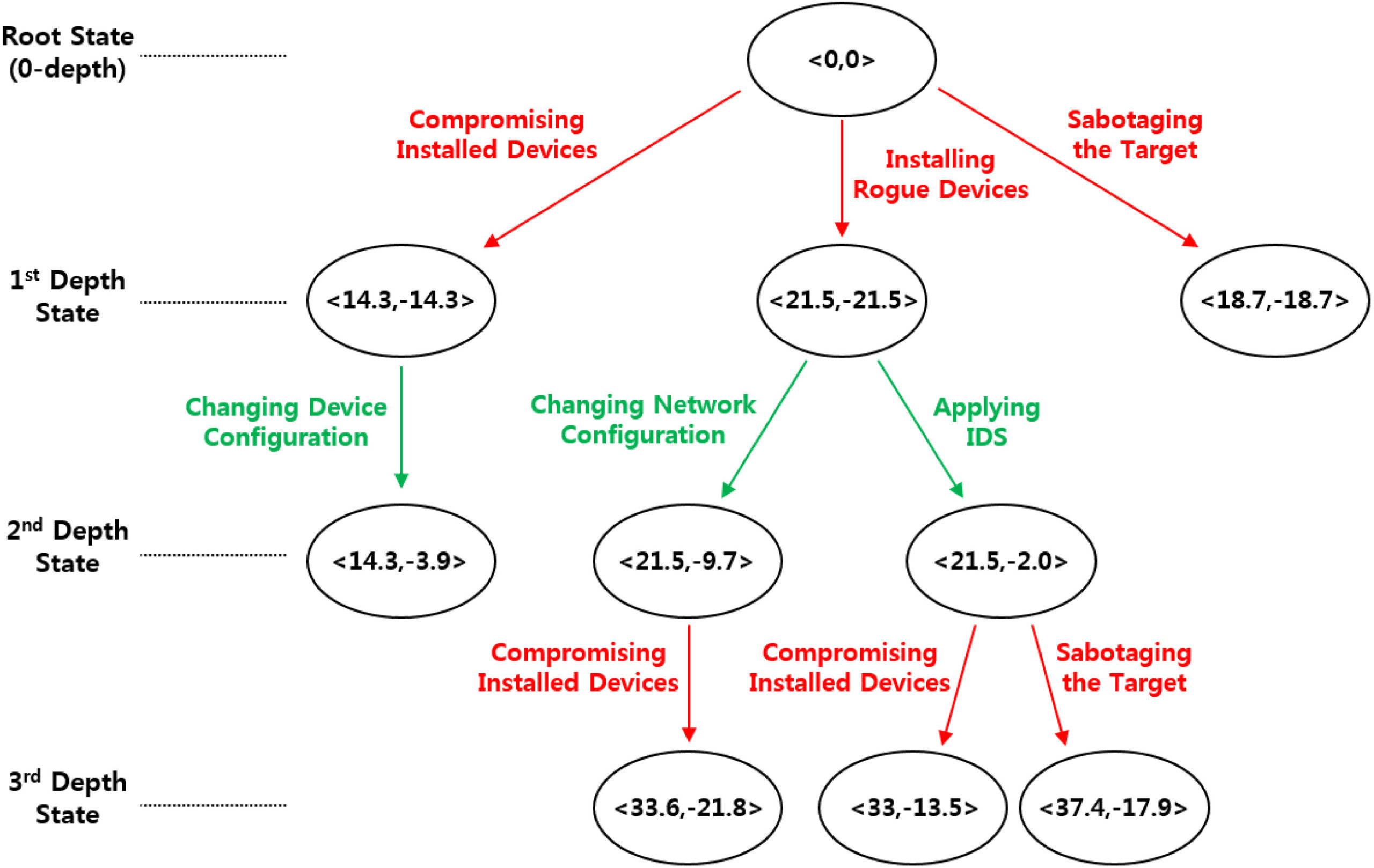
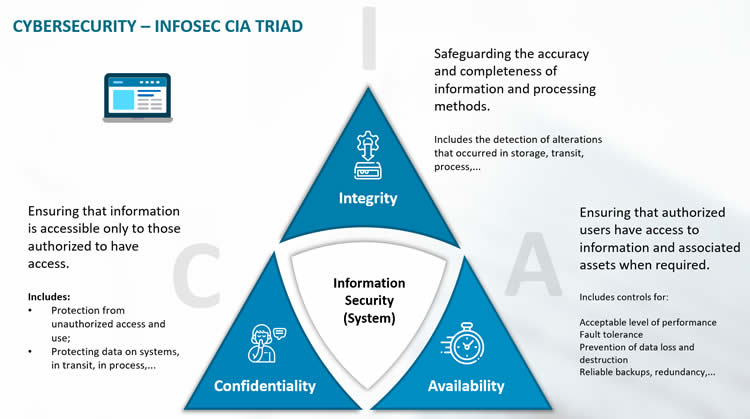
Explanation: Weights on the CIA, and the effect are based on constants defined in the paper using real world data. Each node in the tree is a state of the game <x,y> where x is the payoff thus far for the hacker, and y for the sec-admin. The game tree values are then calculated using the payoff matrix described earlier. As you see, each hacker’s action results in negative payoff for the sec-admin, and the sec-admin then performs a mitigation action in hopes of minimizing the security threats performed by the hacker.
Conclusion
The game tree model that builds upon our foundational knowledge of payoffs taught in class, serves as a better model for the security administrators who have to deal with deciding what mitigations to place against threats. This game theory based approach is more intuitive than a simple risk exposure formula which does not account for the possible moves a hacker can make.
I noticed a few concepts that are clearly missing from the research article that were discussed in class. For example, the talk of a possible dominant strategy the security admin can take to minimize threats (hopefully there is not a strict dominant strategy for the hacker!) and possibility/ a proof of existence of a mixed Nash equilibrium. It would be really interesting to see if there is a game theory based model and article that talks about the existence of a “solution” (provided some simplification to real world scenarios such as the weight vectors for the CIA model in the above description) to minimizing threats which would be nothing short of revolutionary in the field of cybersecurity.
Source
Lee, S., Kim, S., Choi, K., & Shon, T. (2017, September 15). Game theory-based security vulnerability quantification for Social Internet of Things. Science Direct. Retrieved November 10, 2022, from https://www.sciencedirect.com/science/article/pii/S0167739X17308440
One reply on “Game theory based risk management analysis for software systems”
As someone also taking D27, I really like how this relates to both courses! Very good read 😀