Introduction
Although baseball is a team sport, it is unique in that the game revolves around individual one on ones of the pitcher and batter of two separate teams. This aspect of the game is the perfect application for game theory, as both the batter and pitcher know everything about each other, such as the type of pitches and velocity a pitcher throws or the weak points of location and pitches a batter struggles with.
3-0 Count Game
In any batting count, we can simulate a game of whether the batter decides to swing or not swing at a pitch and whether the pitcher throws a ball in the middle or at the corner. For this example, we’ll consider a 3-0 count because at this point, if the pitcher misses they reward a walk to the batter. This game between the batter and hitter can be modelled as such.
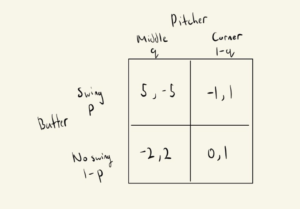
In this game, if the batter swings at a pitch located in the middle, their payoff is at its largest (5) as they most likely get a hit. However, if they swing at a corner pitch, the chances of them getting a hit is low so the payoff is negative (-1). If the hitter decides to not swing at a pitch located in the middle, they lose a good pitch to hit resulting in a negative payoff (-2). If the hitter decides to not swing at a pitch in the corner, they either get a walk or get into a 3-1 count. These two cases neutralize each other resulting in a payoff of 0.
For the pitcher, if the pitcher throws a down the middle while the batter is swinging, their payoff is negative (-5) as they most likely give up a hit. If they throw one at the corner while the batter is swinging, they most likely get a whiff resulting in a positive payoff (1). If the pitcher throws down the middle with no swing, then they have fooled the batter and got a strike resulting in a positive payoff (2). If they throw down the corner with no swing, depending on where the pitch is located they get or strike or give a walk. We give the benefit of doubt that the pitcher throws a good pitch resulting in a positive payoff (1).
Nash equilibrium in a 3-0 Count
In the game above, the pitcher’s expected payoff for a ball in the middle is (-5)*q + (2)(1-q) = -6q + 2, while the expected payoff for a ball in the corner is (1)*q + (1)(1-q) = 1. So. for a Nash equilibrium we must have -6q+2 = -1 with q = 1/6.
For the batter, the expected payoff for swinging is 5*(p) + (-1)*(1-p) = 6p – 1, while the expected payoff for not swinging is (-2)*(p) + (0)(1-p) = -2p. So, for a Nash equilibrium we must have 6p – 1 = -2p with p = 1/8.
Thus a pitcher should throw down the middle 1/8 of the time and at the corner 7/8 of the time, while a batter should swing 1/6 of the time and not swing 5/6 of the time.
Conclusion
This example of a 3-0 count in baseball is stripped of many other important factors when deciding on locations and swinging. For example, the payoffs can vary depending on the type of player and how good they are at hitting balls in the middle or corner. Another variance that determines payoff is how long the pitcher has been pitching for and if they have command over their pitch locations. Nonetheless, at its core, game theory is applicable in determining the best course of action for both the pitcher and batter.
Sources
Micahmelling@gmail.com. (2018, March 16). Game Theory Applications in Baseball. Baseball data science. Retrieved November 10, 2022, from https://www.baseballdatascience.com/game-theory-applications-in-baseball/