To Lead or not to Lead, that is the Question: Game Theory in Race Strategy

It’s race day at the track and field championship and you’ve finished warming up for your 10km race event taking place in 10 minutes. You suddenly remember that you’ve forgotten to decide on a racing strategy! Should you conserve energy in the first half then sprint the remaining laps, or set a fast and consistent pace? All these questions begin to cloud your mind until you realize you’ve studied game theory in CSCC46 with Ashton and all your worries subside…

Background & Motivation

Winning long distance track events in recent years has become increasingly reliant on a runner’s strategy as physical skill across the field has converged. In order to win certain championship races, the runner must pass the finish line first rather than finish with the best time from start to finish. This brought rise to one such strategy called the “sit and kick” where runners will “sit” and conserve energy for the majority of the race, expend all remaining energy in an all out sprint to the finish called the “kick”. One can begin to dissect the factors that make up a winning race strategy using game theory.

Analyzing sports may seem unimportant as an application of game theory when classic examples may include issues of economic competition or morality, but sports provides a forgiving medium to test theories on situations that often parallel ones in business, politics and the greater society.

Analysis

In order to analyze such strategies, we must create a game theory model that describes the strategies available to players. Consider two players (runners) each with two options: to lead the race or to not lead the race. The payoffs associated with each strategy can be organized as such:

It is not immediately obvious why such payoffs are assigned until we consider real life situations of running. In many racing sports such as cycling, auto racing and running, the individual not leading will benefit from sitting in the leader’s “slipstream” which is an “area behind the leader with lower pressure and air resistance, causing the follower to use less energy to move at the same speed” of the leader.

This is modelled here as a payoff of 2 to the player who chooses “Not Lead” as they benefit from the slipstream. The leader gains a smaller payoff of 1 for controlling the pace, though less than the follower.

As in class, we can find the Nash Equilibria in this game:

which we have learned represents the optimal responses for each player given the other’s strategy. This is important as it sets the precedent that each player shouldn’t have any strong incentive to immediately deviate from their respective choices even though both would be better off fighting to stay in the other’s slipstream. This payoff matrix can then be represented as a game tree where player one makes the first choice.

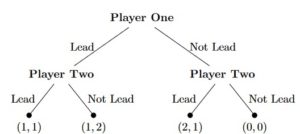
This tree also highlights how neither player has a dominant strategy, and instead has a best response to each of their opponent’s moves.

From class we learned that “a game is played once and players select strategies simultaneously and without consulting one another”. But what happens if we allow players to consult each other in this game?

Racing strategy in real life relies on collaborative efforts that are not considered “optimal strategies” in game theory. Two runners may choose to take turns “pulling” the other via a slipstream, where both runners would conserve more energy overall and be able to sprint faster and longer to the finish line. This is an important limitation of the study as runners in a race typically make split-second decisions on their position many times over the course of a race while being able to see other racer’s decisions.

Conclusion

While these strategic ideas fit nicely into a two player game, there are many more factors deciding a race winner. Some of these factors include: other runners, athletic ability, lap times, and the proportional amount of payoff by sitting in one’s slipstream. These topics could help to produce a more accurate model, while also incorporating running specific data such as oxygen uptake (VO2max). This paper helps set a foundation for the discussion on running race strategy and provides suggestions for future research.

Read more about the paper here!

References

Wheeler, J., & Haas, C. (2018). Game Theory: Analysis of Championship Style Racing.