Introduction
Fighting games provide a fantastic framework for exploring Game Theory as interactions between player options have a very clear payoff structure in terms of damage dealt to the players. Moment to moment, players make several offensive and defensive options, each of which have counterplay which may or may not be situational.
Lagang (2019) explores this idea of offensive and defensive counterplay in terms of Game Theoretical Payoff Matricies with the character Josie in the fighting game Tekken 7. Lagang focuses on a subset of the offensive options that Josie has at her disposal and describes the expanding payoff matricies as the defending player considers more defensive options. By analyzing Josie’s interactions with Game Theory, Lagang (2019) finds a mixed strategy equilibrium in those interactions to try and find ways to improve his gameplay.
This subject is interesting as the strategies employed by Lagang to improve his gameplay can be applied to any other fighting game whether it be Street Fighter, Guilty Gear, or any other game.
I chose to write about this topic as I am very interested in fighting games. I love to discuss strategies and compete against my friends in my free time. Often times, discussions and gameplay revolve around these “RPS” situations which map incredibly well to the game theory topics in class. I think that using game theory to represent fighting game interactions can help players better understand the risk/reward of their decisions to then become better players and competitors.
One of my favorite fighting game content creators heavily discusses the concept of “RPS” in Guilty Gear Strive, my current favorite fighting game. Thinking about fighting games in terms of these game theory concepts help me better understand their teachings about “RPS”.
Analysis
Lagang (2019) considers the situation when the defender blocks one of Josie’s attacks. Josie has four offensive followup options which are Switch 1, Switch 2, Switch 3, and Switch 4.
For the defender, their options involve, standing while blocking, crouching while blocking, or a fast attack (jab) or slow attack.
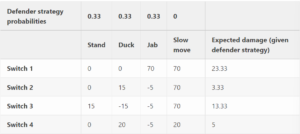
The payoff values are the damage dealt by Josie to the defender. Positive values mean that the defender takes that much damage. Negative values mean Josie takes damage when the defender punishes Josie for picking the wrong option. The payoffs for the defending player would be the negative of the payoffs seen for Josie.
Evidently, there is no pure strategy nash equilibria in this payoff matrix. This means that every option has a counter play from the other player. Said counter play also has counter player much like in Rock Paper Scissors (“RPS”). As a side note, in this way, “RPS” is a term used to describe these sort of fighting game interactions.
To understand why some of these matrix entires, I will go through some examples:
-
(Switch 2, Duck) = 15
Switch 2 is a MID attack meaning that to block it, the defender needs to be standing. When the defender ducks, they take 15 damage.
-
(Switch 2, Stand) = 0
Since the defender stands, they are able to block it properly.
-
(Switch 3, Duck) = -15
Switch 3 is a LOW attach meaning that to blcok it, the defender needs to be ducking/crouching. When the defender ducks, they are able to punish Josie with an attack as a reward for blocking correctly.
-
(Switch 1, Slow move) = 70
If the defending player uses a slow move, the defending player will be hit by Switch 1 before their move can come out and land on Josie. As a result, the defending player gets hit during their move which results in a counter hit. Josie can capitalize on this can perform a large combo to deal 70 damage.
The payoff matricies also display the expected damage when the defender picks randomly. By looking at this payoff matrix, both players can make more informed decisions about their gameplay and pick riskier options less frequently.
Lagang (2019) continues to describe how a more optimal player would play in these situations. More specifically, the defending player can calculate the mixed Nash Equilibrium in the situation to ensure that Josie does not deal more damage when picking a certain switch option.
He provides an updated payoff matrix: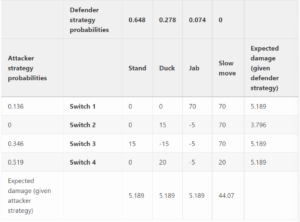
This time, we can see the optimal probabilities for each option for each player. By analyzing this matrix, a Josie player can figure out how to most optimally play their character in this situation, at least in a game theoretic sense.
By applying this method of using payoff matricies and calculating mixed strategies for fighting games, players can better figure out optimal gameplay strategies when attacking or defending with different games and different characters.
When competing in tournament, a player can analyze an opponent’s past matches and count their defensive and offensive option frequencey to then calculate the probabilities for each option. Using payoff matricies and calculating expected payoffs, a player can figure out the probability for each option to best exploit their opponents habits.
Conclusion
By adopting this game theoretic approach to analyzing fighting game player interactions, we can learn that aspects of gameplay can be optimized through game theory analysis even as player skill level increases and the options available become more complex.
In future studies and analysis, various other types of payoff matricies can be drawn. Advantage in fighting games is not purely defined by the amount of health (damage dealt in payoff) a player has. Advantage in a fighting game can be described as frame advantage, screen position, or other game resources depending on the game.