Last year, a Korean drama called Squid Game came out and quickly gained immense popularity. It features 456 characters who are so down-on-their-luck that they would rather participate in a contest consisting of deadly versions of several children’s games on the off-chance of getting rich than continue to live in poverty. Of course, game theory comes in during each game (and outside games), as players have to quickly make decisions that would grant the highest chance of survival. In particular, there are situations in which players have to worry about other players’ possible decisions while making their own, leading to instances of the well-known concept, Prisoner’s Dilemma. This often takes its most intense form when players are given the chance to directly and lethally turn on each other and have to think whether to do so or not. Major instances include the surprise dormitory riot and the final game (I will also speak about the night before the final game, though that does not include Prisoner’s Dilemma). However, while using game theory to analyze these situations, we will see that extraneous variables (especially human emotion) can lead to results greatly differing from what people might have predicted.
In the dormitory riot, everyone must try to survive, whether by teaming up with people, killing people, or both. In this situation, players would have to be careful when trying to team up with others. Should they betray their new teammates? Would their new teammates betray them? The source I read simply categorizes people as either nice people or psychopaths, who have different views of the best and worst outcomes, regarding them and one other person at a time.
A nice person (who apparently feels better about betraying someone if the latter betrayed them too) would consider mutual loyalty the best outcome, followed by mutual betrayal, then them being the sole traitor, then the other being the sole traitor. A psychopath (who apparently sees any outcome involving being betrayed as worse than any not involving it) instead considers being the sole traitor the best outcome, followed by mutual loyalty, followed by mutual betrayal, followed by the other being the sole traitor. Consider values 1-4, where 1 is what someone sees as the worst outcome while 4 is what they see as the best. There are 3 possible matrices (for simplicity, we will only consider Nash equilibria involving pure strategies):
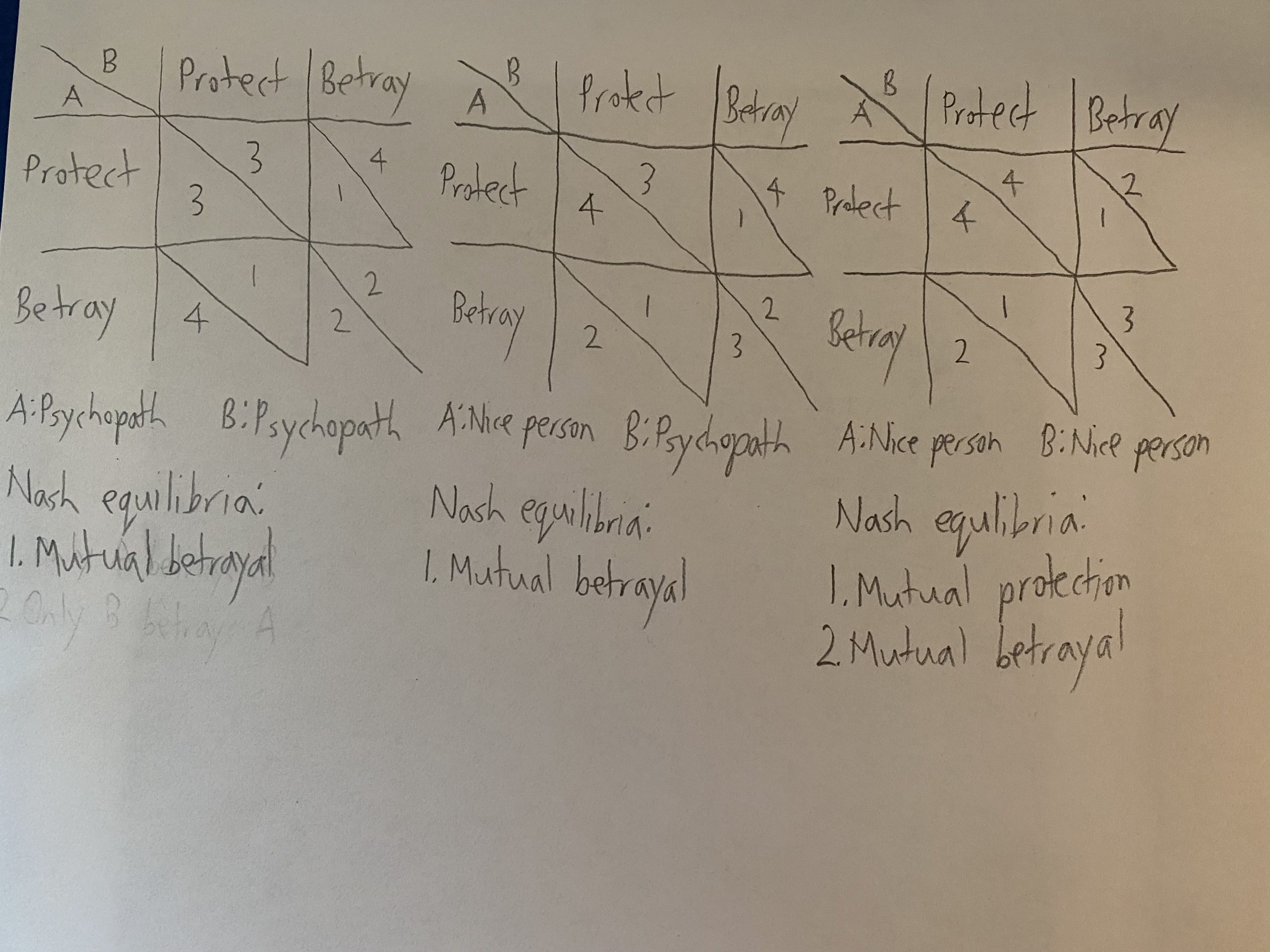
In all 3 possible matrices, mutual betrayal is a Nash equilibrium (in the third case, fear of protecting a traitor would be a focal point encouraging mutual betrayal over mutual protection), meaning we should expect any new alliances between pairs of players to quickly break apart. Yet in the show, we do not see any betrayals in the actual riot, since the crew of protagonists establish a strong enough bond and have no intention of killing anyone at all (for the time being), the gang of antagonists are gladly killing anyone outside their group but not each other (only for personal gain and for the time being), and minor characters show no intentions of deceit but rather open hostility to anyone, likely out of panic at the unexpectedness of the riot, not helped by the constantly flashing lights.
We make a big jump to the night before the final game. Only 3 players remain, and are rewarded with a nice steak dinner. When the servers clean up afterwards, they let the players keep the knives. Clearly they can choose to fight or wait until the final game. In theory, each player would compare the chances of surviving a fight to those of surviving the final game if it happens. They would need to decide just what the former are, while assuming the latter would be ⅓. If the former is higher, they should attack, and otherwise, they should wait it out. Remind you, this is just a theoretical depiction of what would likely happen without additional variables. What actually happens in the show is that one player intends to kill another out of disgust at the latter having crossed so many lines in previous games, yet the third tells him not to, as he is better than that. However, the third herself (who turns out to have been injured from the previous game) gets killed by the second when the first is looking away and calling for medical help for the third (note his selflessness). The first gets even angrier, and guards step in to prevent further violence (despite the fact they initially encouraged it).
The next day, the first and second compete in the final game, still allowed to keep their knives for some reason. This means they can either choose to play the game properly (which involves crossing or guarding drawn boundaries), or just slash and stab each other. In the former, chances of a certain player surviving are ½ since either they live and the other dies, or they die and the other lives. In the latter, it’s only ⅓ since there’s the possibility that both inflict mortal wounds on each other. Knowing this, players can agree to drop their knives together to increase both’s chances of survival, but can suddenly choose to pick up a knife to increase their own further while lowering the other’s. We once again use values 1-4 (4 being the best for a player), and treat everyone equally, as now whether someone is a nice person or a psychopath, they must defeat the other player and they know it. We have the following matrix (and once again only consider Nash equilibria for pure strategies):
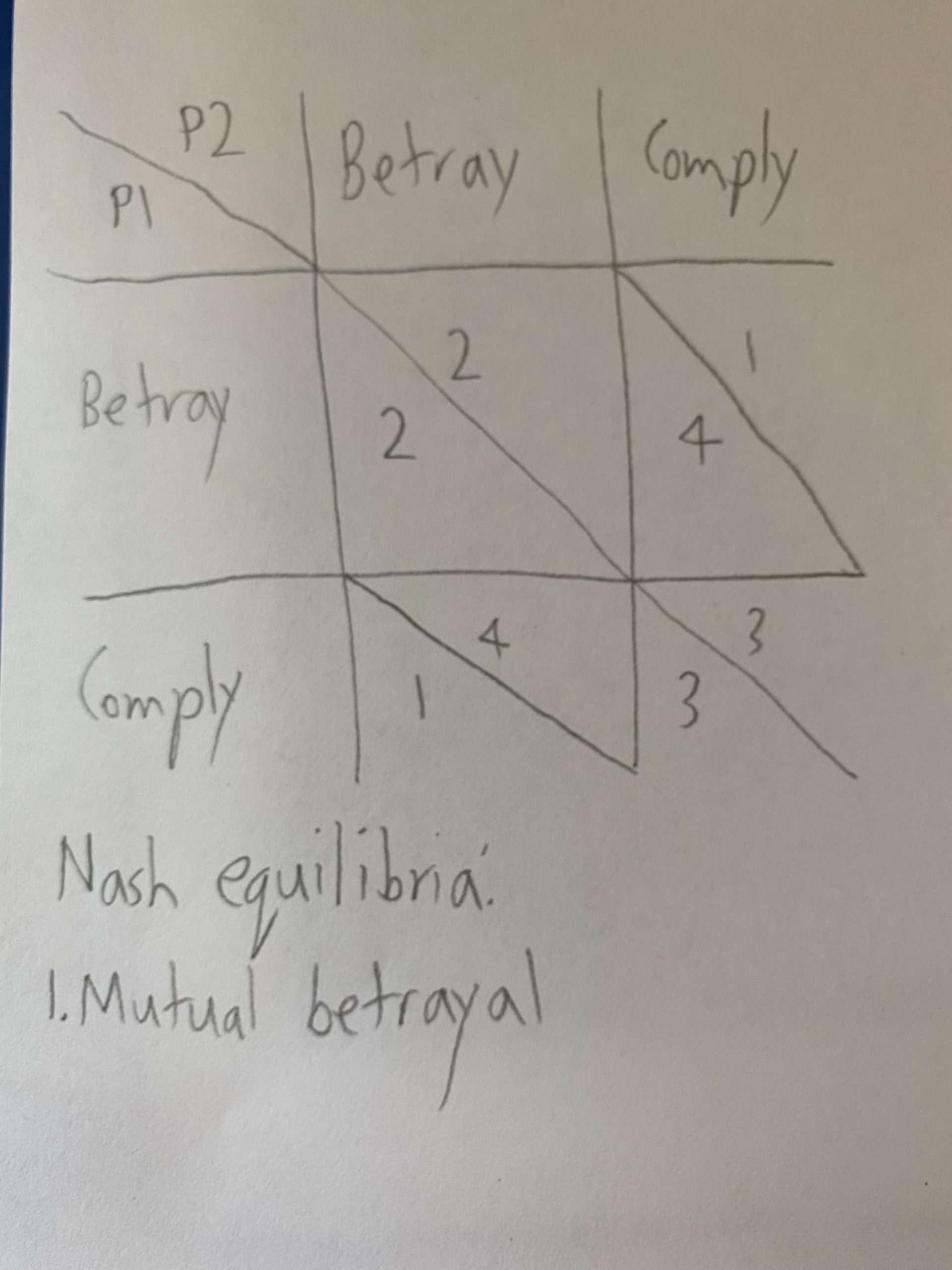
It seems players would most likely betray each other. However, this assumes a sole betrayal is a huge advantage. Players can instead agree to walk away from the knives in sync, such that if one decides to betray the other, the latter has enough time to reduce it to nothing more than a slight headstart, either by grabbing their own knife too, tackling the traitor, or struggling to get the traitor’s knife off their hands. Any of these would make both players more tired, which is worse for both of them. Now we have the following matrix:

Similarly to the dormitory riot, fear of complying with a traitor would be a focal point making mutual betrayal more likely than mutual compliance. Yet once again, I must say this is all theoretical, assuming no outside variables. In the show, the two players do not even consider dropping their knives. The first seeks vengeance for the night before, while the second now has no qualms about directly killing someone to achieve his goals. However, after a brutal fight in which the second is at the first’s mercy, the first, thinking back on what the previous night’s victim had said to him as stated before, decides he does not want any more deaths happening, so he tries to call off the game so both players can live (though without the prize). However, the second kills himself because he realized what he’s become, but also so the first could receive the prize and support both their families (as the two knew each other before the contest).
If people were simply driven by logic, it would be easy to predict what they would do in these games. However, as we see, people tend to be influenced a lot by their emotions (especially in a death contest whose games deliberately mess with them even further), and this could easily change the outcome, while making it difficult to predict what the outcome would be. Of course, there are many other situations where this could happen, even non-deadly ones (such as non-deadly versions of this contest’s games). While game theory is undeniably extremely useful, we must still acknowledge its situational weaknesses.
Source: