1. Introduction
People are addicted to social medias, but why?
I believe that everyone in this class has used one or at least one social media (like TikTok, Instagram, Facebook,…), but have you ever wondered why people usually get so attracted to these apps so much? Among that much information, people are constantly fed with the most attractive ones and undoubtedly, people spend hours scrolling their screens and tapping to interact with them. The more one plays with that, the better one gets fed with attractive posts/videos.
Recommendation systems are crucial in mitigating the information overload problem in social media by suggesting relevant information to users. In this blog, I will share how a signed social network could be an asset under certain scenarios in helping build a smarter recommender. Also, I will attach a recent paper by Arizona State University, Yahoo Research Lab, and IBM Research Centre and briefly introduce what happened there on a framework the authors built and named “RecSSN”. [1]
2. What is a recommender system?
Loose definition on a recommender system
Loosely defined, a recommender system is a system that predicts ratings a user might give to a specific item. These predictions will then be ranked and returned back to the user. Speaking in the world of data, a recommender system is nothing more than a trained model which takes user behavior as input and outputs the predicted recommended items.
They’re used by various large-name companies like Google, Instagram, Spotify, Amazon, Reddit, Netflix, etc. Because of the matter of blog length, here’s a link to the Recommender System on Wikipedia FYI.
3. Signed v.s. Unsigned Social Networks
Comparison between signed and unsigned social networks.
Nowadays, based on research [2] by the team led by Jiliang Tang (also the author of the above paper), the vast majority of recommender systems focus on unsigned social networks (or social networks with only positive links); however, social networks in social media can contain both positive and negative links. It was mentioned during the lecture that Signed Social Networks could be used in recommender systems but we did not have a chance to go really deep into this. In this section, we will see how Signed Social Networks perform better than Unsigned Social Networks.

A lot of research has suggested that in real-world social systems such as eBay (there are many other examples, and trust/distrust websites are most commonly known applying signed social network, here eBay is just the most well-known one), negative links in signed social networks are at least as important as positive links [3]. Comparing to positive links, negative links tend to be more noticeable and credible, and weighed more than positive links of a similar magnitude [4]. For example, negative links add a significant amount of knowledge than that embedded only in positive links [5] and a small number of negative links can improve the performance of positive link prediction remarkably [3].
Evidence from recent achievements in signed social network
analysis suggests that negative links may also be potentially
helpful in recommender systems, and the result given by J. Tang had verified this.
4. Is Unsigned Always Better?
If unsigned social networks are always better, why? Or why not?
I believe most of you started questioning on this and just got an answer of NO as soon as you see the title of this section. Indeed, unsigned networks are not always better, but WHY?
Although it had been shown that using +/- links may create a better performance than only using + links, we see that in most signed social networks, statistics [1] showed that (i) positive links are denser than negative links in signed social networks; (ii) not all users in signed social networks have negative links; and (iii) the user-item matrix is very sparse.
Given that we need heavy data on training the models, the sparsity of negative links in signed social networks may sometimes bring bias.
proposed improvement
Considering the sparsity mentioned above is caused by a lack/missing of negative links, I had come up a method on improving the signed social networks recommender system. I noticed that none of these datasets used in the statistics data are not forcing users to give a feedback and are not anonymous, not forcing causes lack of reviews/links in general, while not anonymous may prevent users from giving negative feedbacks as they intended to do.
Hence, naively speaking, if we could force anonymous feedback, ideally, we could have a “better” signed networks to train the recommender system.
5. RecSSN Explained [1]
You can skip this section if not interested.
I couldn’t find a way to insert math formulas, so I just did it in raw texts as I would do with LaTex, this heavily affected the readability, so feel free to check the original paper, sorry to the audience for the inconvenience.
The authors of the papers, Tang, Aggarwal, and Liu created a framework called RecSSN when comparing the performance of the recommender systems on signed social networks vs unsigned social networks. In this section, I will introduce how they build such framework, what datasets they used, and the algorithms they proposed. (Note that this section may involve lots of mathematic formulas)
The experiment is mainly based on two datasets: Epinions and Slashdot, with details mentioned in 5.2
5.1 Problem setting
Given observed values in R and a signed social network G
with positive links A^p, and negative links A^n , the problem of recommendation with a signed social network aims to infer missing values in R.
Let U = {u_1, u_2, . . . , u_N} be the set of users and V =
{v_1, v_2, . . . , v_m} be the set of items where N and m are the
numbers of users and items, respectively.
We assume that R ∈ R^(N×m) is the user-item matrix where R_ij denotes an observed score (has different meaning based on datasets) from u_i to v_j and we set R_ij = 0 if the score from ui to vj is missing.
We use A^p and A^n to denote the adjacency matrices of positive and negative links, we will have A^p_ij = 1 if there’s a positive link between user u_i and u_j, similar setting applies to A^n.
5.2 Data sets

- Epinions is a popular product review site. Users in Epinions can create both positive (trust) and negative (distrust) links to other users, which results in a signed network G. They can also rate various products with scores ranging from 1 to 5. Therefore, if u_i rates v_j, R_ij is the rating score, and R_ij = 0 otherwise.

- Slashdot is a technology news platform. Users in Slashdot can create friend (positive) and foe (negative) links to other users, which results in the signed network G. They also can specify tags associated with them. Therefore, if v_j is associated with u_i, R_ij = 1, and R_ij = 0 otherwise.
- Preprocessing of datasets is not mentioned in the paper, but I believe they just did some formatting and cleaning.
5.3 algorithms
An optimization problem that uses the same idea as optimizing a decision tree in machine learning
They converted the problem into an optimization problem, due to the volume of formulas they had and that I wasn’t able to type math formulas, I will introduce the key points. You could have a look on the paper that created the framework [1] or another one [5] that surprisingly derived same formula
- Gradient Descent
- Commonly used in solving optimization problems
- An algorithm in finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (direction of derivative) of the function at the current point, because this is the direction of steepest descent.
- Similar idea applies to finding local maximum.
- It played an important role in the present algorithm of RecSSN as we always needed to find the local maximum/minimum to optimize the solution.
- Goldstein Conditions / Backtracking Line Search
- A line search method to determine the amount to move (in this case, during gradient descent) along a given search direction.
- The learning step in the algorithm are specifically restricted by this backtracking line search method.
- Optimization
- Randomly assign the initial values, and then gradually evolve based on gradient descent under steps from Goldstein Conditions.
 Step 1: The paper initialized the two output matrices U and V as the user preference matrix and the item characteristic matrix, respectively.
Step 1: The paper initialized the two output matrices U and V as the user preference matrix and the item characteristic matrix, respectively.
Step 2: Derive a formula to check convergence, and an objective function named J.
Step 3: Update U and V with the gradient within learning step determined by Goldstein Conditions.
Step 4: update gradient using multivariate derivatives
Step 5: repeat step 3 and 4 if not convergent.
5.4 result
We will discuss what metrics had been used and what they showed, Again, feel free to check in the paper.
- Root Mean Square Error (RMSE)
- Measures the square root of the squares of the differences between predicted values and observed values.
- The lower, the better
- Mean Absolute Error (MAE)
- Measures the average of the squares of the errors
- The lower, the better
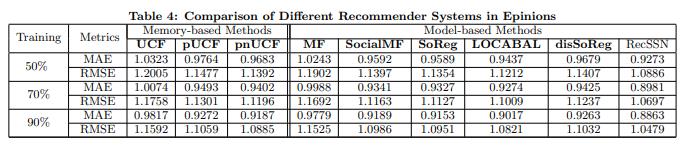
We see that RecSSN performs better than other models in terms of RMSE and MAE on Epinions.
- Precision (P)
- P = True Positive / (True Positive + False Positive)
- Although higher is better, but need to take a look with R.
- Recall (R)
- R = True Positive / (True Positive + False Negative)
- Although higher is better, but need to take a look with P.

We see that RecSSN performs better than other models in terms of Precision and Recall on SlashDot.
6. Conclusion
Great potential on better connecting people
Recommendation systems are crucial in mitigating the information overload problem in social media by suggesting relevant information to users. The vast majority of recommender systems focus on unsigned social networks (or social networks with only positive links). However, social networks in social media could contain positive and negative links and little work exists for recommendations with signed social networks. The leveraging of negative links for recommendation is a challenging task because straightforward extensions of unsigned networks do not seem to be applicable in this case. But once we build a fitting framework on signed networks, it soon outperforms the frameworks on unsigned networks (under specific cases). I firmly believe that mining signed networks are still in its early stage; thus as researchers investigate more applications in signed networks, there would be a huge improvement for social media to build better connections.
7. References
This blog is greatly based on and adapted from research done by Jiliang Tang, it may be biased as it is mostly from one author.
[1] Jiliang Tang, Charu Aggarwal, and Huan Liu. 2016. Recommendations in Signed Social Networks. In Proceedings of the 25th International Conference on World Wide Web (WWW ’16). International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, 31–40. https://doi.org/10.1145/2872427.2882971
[2] J. Tang, X. Hu, and H. Liu. Social recommendation: a review. Social Network Analysis and Mining, 3(4):1113–1133, 2013.
[3] R. Guha, R. Kumar, P. Raghavan, and A. Tomkins. Propagation of trust and distrust. In Proceedings of the 13th international conference on World Wide Web, pages 403–412. ACM, 2004.
[4] J. Cho. The mechanism of trust and distrust formation and their relational outcomes. Journal of Retailing, 82(1):25–35, 2006.
[5] M. Jamali and M. Ester. Trustwalker: a random walk model for combining trust-based and item-based recommendation. In Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 397–406. ACM, 2009.