The holiday season is just around the corner. Everyone loves spending time with their friends and families doing fun activities like cooking and watching movies. Gift exchanging games is a fun activity that many do during the holiday. With any gift exchange, the real goal is to win the best gift.
The payoff matrix below represents a normal gift exchange between 2 people. E represents the enjoyment the player feels when they get a gift. C represents the cost of the gift the player gives. As we learned in class, we can apply nash equilibrium to see that both players will choose to receive, as it’s the dominant strategy for both players. Assuming the enjoyment is greater than the cost, the payoff is like the prisoner’s dilemma. So there is no winning here.
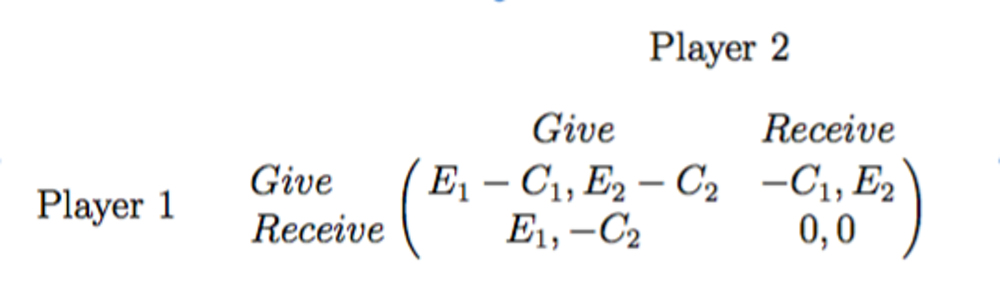
White Elephant gift exchange, also known as Yankee swaps is a variation on Secret Santa. Everyone brings a wrapped gift to the party and leaves them in the middle. Then everyone is given a random number which is the order in which everyone picks a gift. The first person picks a gift and opens it. The player after then makes a choice to either pick another gift and open it or steal a gift that has already been opened. If the player decides to steal the gift from someone, then the player whose gift got stolen will have a chance to steal another gift or choose a wrapped gift. A player can’t steal a gift that just got stolen from them and a gift can only be stolen a certain number of times. This gift exchange finish after all players have played and all gifts are opened.
The best scenario would be to go last, so if you want to steal you have the most variety of gifts to choose from. However, you don’t get to choose the order you play, but you can always pick the best strategy. Ben Casselman used basic game theory questions (such as Should you always steal? Never steal? Steal only under certain circumstances?) to come with steps to get the best gift. He tested the following 8 strategies:
- Player steals with probability p = (number of gifts taken) / N (naive).
- Player always steals most valuable gift available.
- Player always steals second-most-valuable gift available (if only one gift is available, player steals that one).
- Player never steals.
- Player steals if any stealable gift has value (to them) greater than the mean value of all opened gifts.
- Player steals about-to-be unstealable gift (steals == max.steal – 1) if one is available with a value greater than the mean value of all opened gifts.
- Same as #5 but factor in knowledge of the gift the player brought.
- Player steals if best available gift has value > expected value
Running the model resulting in the follwoing:
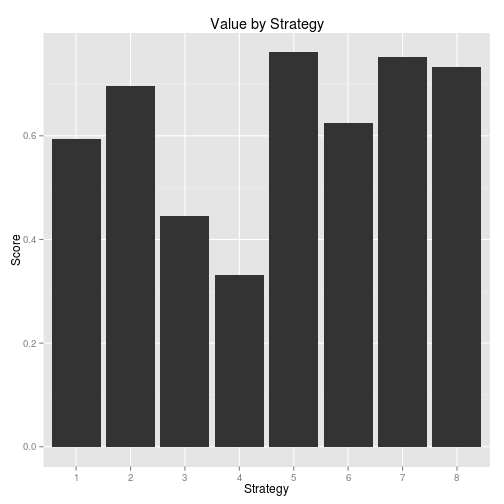
Using that result, Ben came up with the following step for the best strategy:
- As each gift is opened, mentally assign it a value (perhaps a dollar value or a 1-to-5 ranking);
- When it’s your turn, average the value of all the opened gifts (whether or not they’re available for stealing);
- If there is a stealable gift “worth” at least as much as the average, steal it! Otherwise, open a gift. (Depending on the rules you’re playing by, not every gift might be available for stealing.)
Happy swapping! Hope you get the best gift!
Sources:
https://theconversation.com/how-to-apply-game-theory-to-buying-your-christmas-presents-52233
https://github.com/BenCasselman/YankeeSwap
https://fivethirtyeight.com/videos/white-elephant-yankee-swap-game-theory/