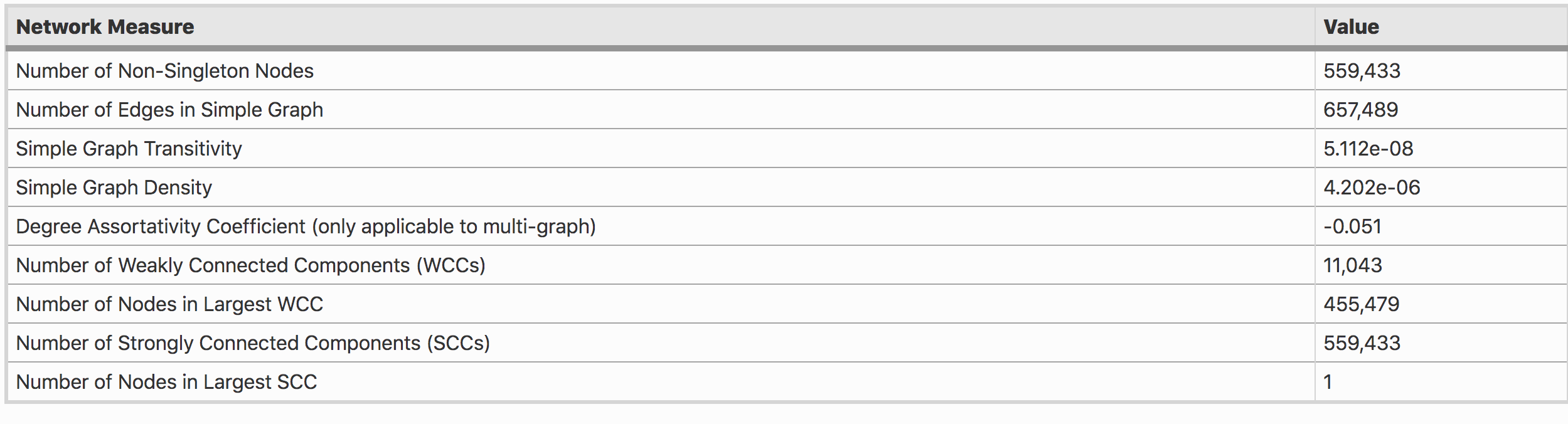
Rashida Mustafa Kapadia – CSCC46 2020 Course Blog

Warning: Spoiler alert!

As some of you may remember, the movie ‘Crazy Rich Asians’ is about a Chinese-American economist from New York named Rachel Chu who visits Singapore with her boyfriend, Nick Young. While in Singapore, Rachel meets Nick’s crazy rich Singaporean family, including his disapproving mother, Eleanor.

In the climax of Crazy Rich Asians, we see that Rachel plays mahjong with Eleanor. This scene is crucial in determining whether Rachel gets to marry Nick and live happily ever after. Since Rachel teaches game theory as an economics professor, the decisions she makes in this part of the movie are carefully plotted to maximize her payoff. Both characters are also extremely smart and strategic players, which would mean that analyzing their choices on a payoff matrix would turn out to be very interesting (especially in the midst of exam season).

The payoff matrices differ before and after the scene where Rachel and Eleanor play mahjong. Before they played together, Rachel had two choices – stay with Nick or leave Nick. Similarly, Eleanor also had two choices where she could either choose to give the couple her blessings or not do so.

We can notice that if Rachel stays and Eleanor gives her blessings, Rachel’s payoff is a happy marriage to the love of her life. However, Eleanor would lose her son because he’d stay in America with Rachel. If Rachel leaves and Eleanor chooses to give her blessing (a very unlikely scenario), both women lose Nick because presumably Nick will go back to New York City to find Rachel.

Now, this is the interesting part. It’s clear that Eleanor has an erroneous expectation of what Rachel’s payoffs will be since she does not see Rachel as deserving and does not understand how much Rachel loves her son. Without her blessing, Eleanor thinks that Rachel’s payoff for staying is happiness since she gets to marry Nick, and Rachel’s payoff for leaving is heartbreak. For either choice Rachel makes, Eleanor thinks she gets to keep Nick in Singapore. To summarize, their payoff matrices look like this:

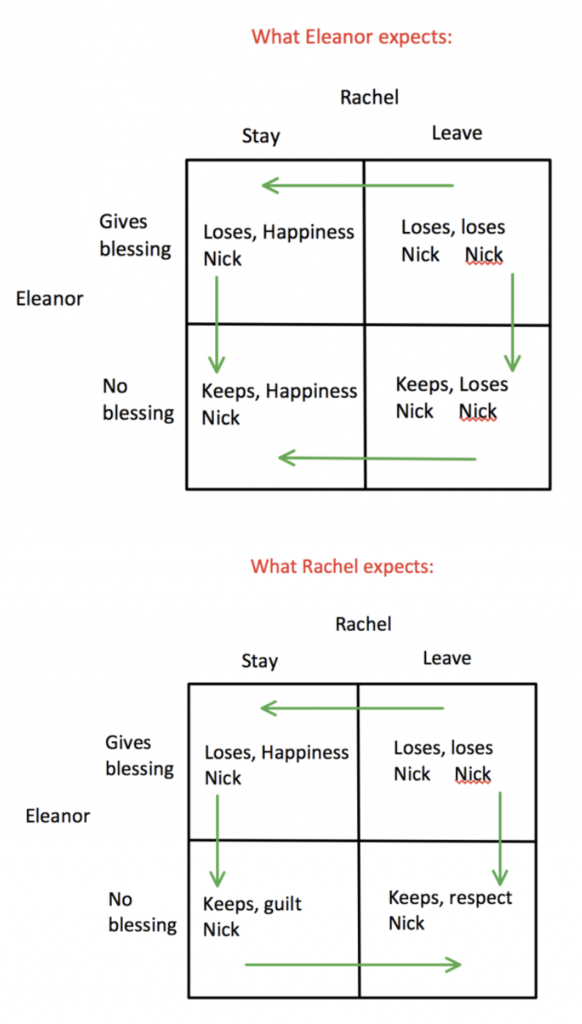
Diagram 1: Payoff Matrices for Eleanor and Rachel

The payoff matrices show that there are actually two different Nash Equilibria due to their different perceptions. We see that Rachel is not willing to keep Nick away from the family and she wants Eleanor’s respect. Since Rachel knows that Eleanor’s dominant strategy is to not give her blessing, she chooses to leave because this gives her a higher payoff as compared to staying with guilt.

There is one more catch in this game. Eleanor finally realizes that she might lose her son forever by not accepting Rachel. This occurs during the mahjong scene where Rachel explains to Eleanor that if Nick chooses Rachel, he’d lose his mother and his family. Additionally, If Nick chooses his family, that would mean he might resent Eleanor forever — thus losing his mother anyways. Therefore, it would be a lose-lose situation for Eleanor. Then, Rachel clearly points out that she decided to seize control of the situation and make the decision for Nick. But she doesn’t want it to happen without Eleanor knowing exactly why it’s happening and what Rachel is giving up to make it possible.

This exchange combined with Rachel’s self-sacrifice changes Eleanor’s payoffs to the following:

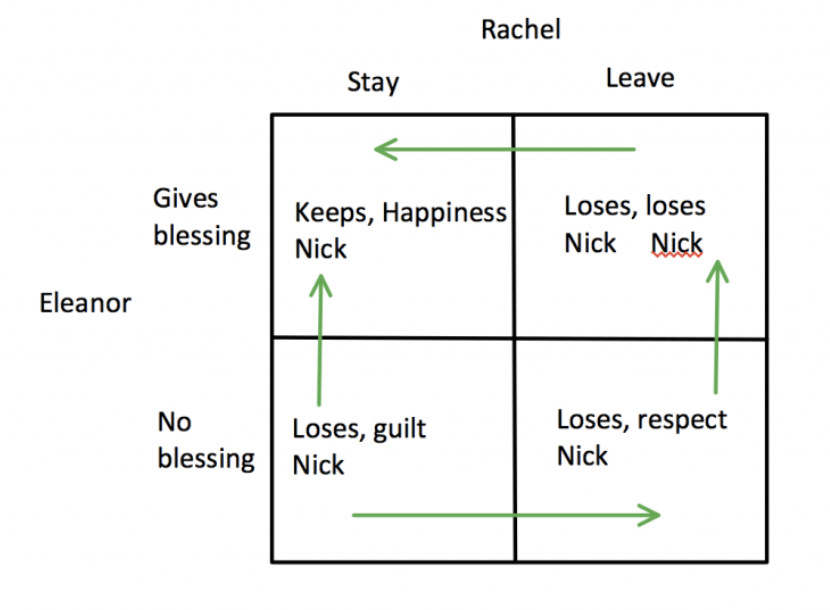
Eleanor realizes that giving her blessing is the only way she can keep her son, so this becomes her new dominant strategy. She gives her blessing to Nick who then proposes to Rachel with his mother’s ring. In the end, game theory works in Rachel’s favour and she gets her happy ending.

Sources:

https://www.npr.org/transcripts/681228147

https://www.vox.com/first-person/2018/8/17/17723242/crazy-rich-asians-movie-mahjong

https://www.imdb.com/title/tt3104988/

Game Theory in Crazy Rich Asians

What would you do if your paycheque was in millions? Perhaps you’d buy a mansion, a Ferrari or pay off all your student debt. But with a lump sum of money comes other big issues, which is why a lot of people decide to hide their money in secure offshore companies. The Panama Papers scandal reached headlines back in 2016 when 11.5 million documents of the world’s fourth biggest offshore law firm were leaked. According to the Guardian, these included accounts pertaining to the hidden wealth of the world’s most prominent leaders, celebrities and politicians such as Vladimir Putin, Nawaz Sharif and several others. While using the services of offshore companies aren’t illegal, the files raise fundamental questions about the ethics of such tax havens – and the revelations are likely to provoke urgent calls for reforms of a system that is arcane and open to abuse.

In our lecture this week, we talked about the ‘six degrees of separation’ and how for any pair of people, there is a friendship path between them. This would mean that it is easy to find patterns that show connections among different people. However, a 2020 research study conducted by an assistant professor, Mayank Kejriwal, concluded that the Panama Papers network of offshore entities and transactions were all disconnected and did not contain any triangular structures. It is precisely this disconnectedness that makes the system of secret global financial dealings so robust. Because there was no way to trace relationships between entities, the network could not be easily compromised. This study was performed with a focus on structure as a means of expressing and quantifying the complexity of the underlying system.

In his research, Kejriwal calculated the density, weakly connected components (WCC) and strongly connected components (SCC) of the network. Table 1 shows that there are no non-trivial SCCs in the graph G (every node falls in its own SCC when partitioning the graph into SCCs). He also calculated the transitivity of G which is the fraction of all possible triangles present in the graph. Transitivity for multi-graphs is not well-defined; hence, it is only shown for the simple network equivalent of the Panama network. Overall, the network is extremely sparse and unlike social networks, the transitivity is also very low.

Figure A: Connected component size distributions of G, G_i, G_o, and G_io. The x-axis is the number of nodes in a connected component and the y-axis is the frequency of that size in the dataset

The above figure shows a lack of connectivity, and a systematic distribution of component size, which is an indication that the networks are dissimilar from social networks which tend to be connected (or almost connected). In other words, the Panama Papers do not seem to exhibit any ‘small-world’ phenomenon.

Table 2 shows that the number of bridge edges in the network are very high (and sometimes extreme in the case of Gi which is 100%). This suggests that every edge in the largest component in Gi is a bridge.

In particular, the lack of small-world phenomena in all selectively constructed and higher-order networks seems to be suggesting that a different theory is at play in this dataset, and that disconnectedness is a fundamental, emergent feature. Assuming the connected components proportionally capture some level of corrupt activity, corruption itself would seem to be a rather robust phenomenon, since targeting a few nodes would not bring the whole structure ‘down’. Even more disturbingly, data suggests that the larger components would also have limited utility in cracking down on overall illicit activity. Finally, we should consider the dynamic nature of entities: offshore companies can quietly and quickly change ownership and beneficiaries in many jurisdictions, intermediaries can be replaced or shut down, and new shell companies can emerge, all in short order. Robustness is, therefore, an inherent feature of this system in more ways than one.

Since small world phenomena did not occur in a single network, and the distribution of connected components seems to follow a clear and consistent trend throughout, it suggests a stark difference between patterns exhibited in small-world networks.

According to Kejriwal, even if you randomly connect things, in a haphazard fashion and then you count the triangles in that network, this Panama network is even sparser than that. He also added, “Compared to a random network, in this type of network, links between financial entities are scrambled until they are essentially meaningless (so that anyone can be transacting with anyone else).”

These reasons are why it is challenging to crack down and trace the network of these systems.

Sources:

https://www.sciencedaily.com/releases/2020/09/200929152152.htm

https://appliednetsci.springeropen.com/articles/10.1007/s41109-020-00313-y

https://www.theguardian.com/news/2016/apr/03/what-you-need-to-know-about-the-panama-papers