No matter how high quality a film is, if it is not marketed properly or released at a right time, it may get hit by low sales. Many things can influence the release date of a film. Genre of a film is one of the most important things that affects its release time as people are used to certain types of movies in certain seasons. That is why we usually get blockbuster action movies in Summer, critically acclaimed dramas in Fall, scary and horror movies closer to Halloween and comedy/holiday theme movies closer to new year holidays. However, genre of a film is not the only thing that greatly has an influence on the release date. Publishers also try their best to make sure they release their films farther apart from each other so that they do not have to compete with each other in box office revenues. That is the reason researchers from Shanghai University of Finance and Economics, decided to explore the idea of using Game Theory in order to see if they can maximize the revenues of multiple studios competing with each other for release time slots and whether or not there exists a pure Nash equilibrium for such scenarios.
In their model, they used n players (film publishers), who are selfish and always trying to maximize their revenue. They decide the release date of the film and only have one film to publish. They used a utility function u_i(a, delta) which defines the number of audience who watches player i’s film.
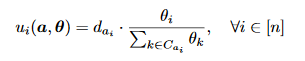
In the function above, a is the action profile. There are M available time slots and a_i is in M. delta_i is the popularity degree of the film i. C_j is the set of players who chose the time slot j. The demand of the audience in j-th time slot is denoted by d_j.
Using the function above, they are able to calculate the utility (revenue) a player earns in each time slot and are able to create a payoff matrix based on the actions each player chooses. After creating the payoff matrix, the researchers then had to prove that a pure Nash equilibrium exists in the matrix. In order to do that they created a set s that defines the strategy profiles of all the players. s_i is the strategy profile of player i, s_-i is the strategy profile of all players except i.
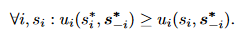
Proving the equation above means that, there is a strategy s^* that no player can increase its utility by changing its release time slot. Therefore, there exists a Nash equilibrium.
Using the utility function and the payoff matrix created by the utility function they were able to prove the above equation which led to this theorem:
“In the attraction competition game, there always exists a pure Nash equilibrium. If players choose the release time greedily in the decreasing order of the popularity degree, the reached schedule is a Nash equilibrium.”
As we saw in the example above, Game Theory can be used to analyze many real life decisions which can lead to better decision making and profit to parties that use it efficiently.
References: