The popular card game of poker has been studied for many years for its various applications of mathematical principles. The complexity of the game along with the addition of several opponents making predicting the winner difficult to approach. The paper written by Jingyu Li focuses on a two-player poker game in which he analyzes the strategies for each player. In order for a player to time, they need either a made hand or a draw hand. In a made hand, the player does not have to wait in order for more cards to be relived to have a winnable hand. A draw hand refers to a hand that can potentially be a winner depending on the drawn cards that follow.
In a real poker game, neither of the players are aware of their opponents’ hands so they must act on implied odds. This allows them to make more money as more cards are revealed later in the game. Every time a player raises the pot or check when the opponent matches. If both players are able to predict each other’s games, they can use their expected value to determine if they should further bet on the given hand. However, in a real poker game, players can bluff on their hands to raise the stakes of the game without having a high probability of winning. This makes it hard for a player to derive a generalized strategy.
In a game like poker, having a fixed strategy leads to diminishing returns over time as the opponent can exploit the strategy by playing predicting your moves beforehand. Therefore, the strategy should be created that focuses on a range of cards upon which you would bet on while folding on anything outside of that range. For example, even if you have a bad hand inside your range, you should bluff on your cards rather than folding. Furthermore, there exists a concept of an indifference in which a player gets the same amount of expected payout regardless of the strategy chosen. This indifference is used with an indifference threshold which allows a player to determine when their strategy is indifferent.
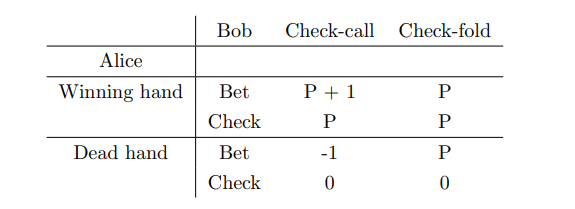
Consider the payoff matrix shown in figure 1. In this case, Alice should always bet when she has a winning hand, regardless of what Bob might have. In this scenario, P refers to the money in the pot that the player wins at the end of the game. When Alice has a dead hand, she has a chance of winning the pot only if Bob chooses to fold. Otherwise, she loses the $1 that she bets on her dead hand that is going to lose. In this scenario, Alice should deploy a bluffing strategy that would make Bob indifferent by picking any of his call or fold options yield the same amount of money. Bob’s strategy on the other hand should be to make Alice’s strategies of Betting or Checking on a dead hand indifferent. Which would make her choose the one that benefits Bob.
Overall, this paper captivates a good strategy that players employ when playing the unpredictable game of poker. They can choose a flexible range to stay within when betting in order avoid being exploited over time by the opponent. However, even such strategies must be mixed with discrepancies in order to avoid being predicted by the opponent. This paper provides a good real-life application of game theory from the material we discussed in class. Many of the great poker players have made their careers in poker because of their ability to exploit their opponents and devise a changing game plan that allows them to win big money.
Reference:
https://math.mit.edu/~apost/courses/18.204_2018/Jingyu_Li_paper.pdf