Author: Aster Wu

Two perfectly rational gingerbread men, Gingerb and Read, are taking a stroll through the forest when a hungry wolf jumps out at them a la Swiper from Dora the Explorer style. The gingerbread men recognize this scenario and chants an ancient spell to protect themselves: “Swiper, no swiping!”. The wolf simply laughs. He could easily eat both of them but is slightly amused at their futile attempt. He proposes a game:

“You have the option to sacrifice or spare the other cookie. If you both choose to spare the other, I’ll eat just one of your limbs. If one chooses to spare and the other chooses to sacrifice, I’ll eat the sparer while the sacrifice is free to leave. If you both choose to sacrifice, I’ll eat 3 limbs each.”

Sound familiar? This is classic example of the Prisoner’s Dilemma. The payoffs are the amount of limbs they’ll have remaining:

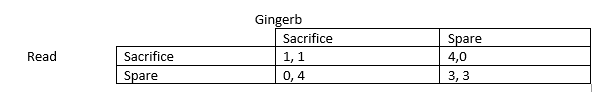
There exists a Nash equilibrium where both gingerbread will always want to choose the sacrifice strategy, so both perfectly rational gingerbread will hobble away having lost 3 limbs and a friendship. Now here’s where it differs.

A secret observer has been watching this situation unfold the entire time. Like a person who chooses to film on their phone rather than help. This bystander uses their magic and teleports next to the gingerbread, loudly shouting “You fools! Why have you chosen such a rational but terrible decision?!”

Gingerb and Read: “Please powerful wizard! Help us get our limbs back?”

Wizard: “I will grow all your limbs back, but at each sunrise I will tell the wolf to come back and history will repeat itself for the rest of your lives!”

Now this has turned into the Infinite Prisoner’s Dilemma. What a fun twist. The gingerbread must now consider what happens in the future in order to make their decision in the present. Let’s see what the possibilities are for these gingerbread now.

If one of the gingerbread decides to sacrifice while the other chooses to spare, the other petty gingerbread will retaliate by choosing to sacrifice for the rest of their lives.

Would knowing this be enough to force these two to choose the spare strategy? We can figure this out by considering a factor δ where 0 <= δ <1, which represents the amount they care about their future limbs. In other words, if δ = 1/2, then on the first day of this sordid situation, they will care about their limbs just as much as they would normally. On the second day, they’ll care ½ as much. On the third, ¼ and on the fourth, 1/8. If δ is 0, this means they don’t care about their future at all which brings us back to the original Prisoner’s Dilemma where both will choose to sacrifice permanently. If δ approaches 1, this means they’ll always spare each other.

Why do they care about their limbs less and less? This dilemma will last forever. While their initial reaction may be to protect their limbs, gradually they’ll become more apathetic as they come to terms with this calamitous chronicle. So, what is the minimum δ required for them to both spare each other forever?

To answer this, we can write the infinite series that represents each strategy, setting them equal to each other and then solving for δ.

If they both choose to spare:

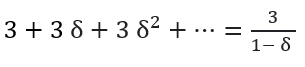
If they both choose to sacrifice:

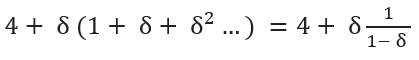
We end up with δ = 1/3.

This means that if they care about the next day at least 1/3 as much as today, the best strategy is to choose to spare each other forever.  

This situation can be compared to real life. The decisions we make today affect the decisions that others will make tomorrow. While some easy and rewarding decisions may seem a lot better, those around you will remember what you have done and may cause you more trouble than you can handle in the future.

Source:

https://youtube.com/watch?v=cWG6UNtSv9I

https://econ.ucsb.edu/~sevgi/EmbreyFrechetteYuksel_June2017.pdf

Some of us are avid music listeners, constantly spending the day listening to playlists and mixes whether it’s for relaxation, for jamming, or as background noise to help us get through a particularly challenging assignment. Some of us also love sharing music with our friends. Inevitably, one might create a playlist containing their current favourites in the hopes that the receiver of the playlist might add a few of those songs into their own. Before sharing them, we’ll commonly preface them with “My playlist might be a bit all over the place. It’s got a little bit of everything so you might not like all of it”. I wanted to know; are the artists I’m listening to really that different from each other? Can we identify communities within the artists I’m listening to? To help me answer this question, I’m using this tool called the “Spotify Artist Network” to help me visualize the network of artists.  For this blog, I’m going to use American alt-rock band Wallows as the root of my network. This is the resulting network.

It is important to note that the clusters represent related artists and not artists who have worked with each other. How does Spotify determine related artists?

The tool does a great job of organizing artists into clusters for us. The root node is in black and the node size and color indicates popularity of the artist. In the center cluster, we have related artists like Conan Gray, girl in red, Beach Bunny, Cavetown, mxmtoon. The sounds of Wallows’ songs are backed with the sounds of snares and crash cymbals and arguably can not be compared to the soft ukulele instrumentals of mxmtoon’s bedroom pop. Despite the difference in sound, Spotify’s algorithm has decided that they are closely related. This may be due to the fact that their songs are commonly used in TikToks, and they’re also popular social media personalities. In a distantly related cluster, we have hard rock artists who are commonly compared like My Chemical Romance, Mindless Self Indulgence, and Pierce the Veil. In another cluster, we have intimate indie-pop artists like Peachy!, Shiloh Dynasty, and khai dreams. All of whom are commonly featured in hours-long lo-fi mixes on YouTube.

Spotify does have an actual answer to the question. In short, Spotify analyzes the number of fans shared by two artists proportional to their total number of fans and also the way they are described on other media (i.e. blogs, magazines, social media). The number of shared fans has a higher weighting but artists getting a surge of attention in the media are also a significant factor. This is clearly shown from the observations above. Some of the clusters are highly connected due to the genre and the common comparisons in media between them. Other circumstances like social media trends and challenges are also heavily influencing how the artists in this network are clustered.

So yes, we can definitely find communities and see how these seemingly disconnected artists share a large portion of the same fans. In addition, using these clusters, we can determine which songs could be classified as a different genre, but we would still enjoy it. Of course, there are also clusters consisting of a single node between clusters so those songs can be seen as an entry to another cluster.

For further technical investigations of Spotify songs and artists, one can look at the Spotify Developer API.

For more information on the “related artists” algorithm, check out Spotify’s blog post: How “Fans Also Like” Works.