https://www.nature.com/articles/s41591-020-1036-8
Here we can see a paper on some simulations, predicting the differences on how COVID spreads throughout a UK town (Haslemere), where they compare the spread between no intervention and contact tracing prevention. In this network graph, each person represents a node and each contact an edge, as shown by the image below.
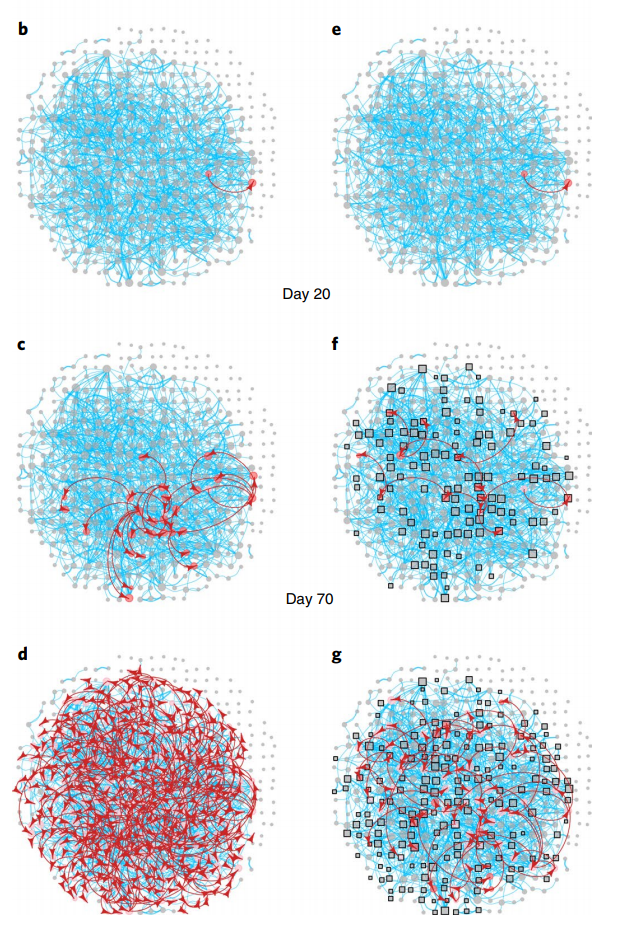
I think it should be fairly obvious that without intervention or prevention, the number of cases explode (left networks), while with contact tracing and quarantine, the number of cases increases but at a vastly slower rate (right networks).
In this graph, we can first see that the graph is not connected: there are nodes near the edges of the circle that come into no contact with any other node, and as expected they never get infected, though this is just a simulation and thus not overly realistic as most nodes come into some sort of contact with other nodes.
However, excluding the outside nodes, we can see that the core of the graph is very much interconnected. While not exactly like a bowtie as in the network of the internet as this graph is undirected (and thus cannot be SCC by definition), we can assume that there is most likely a huge connected core with smaller connected subgraphs scattered around. This of course implies that infections spread quickly with all the interconnected contacts, and indeed as seen on the left simulations it’s what happens.
Consider instead the method of quarantining the infected, as per the right simulations. Although the core of the graph is connected at first, by quarantining various nodes we will eventually (depending on how connected the graph is) segment the huge connected core graph into smaller subgraphs, or more precisely, into different components. This allows the infected to be localized and thus slows down the rate of infection.
Furthermore, by segmenting the graph, we destroy local bridges and this also aids in slowing the rate of infection. Each infected node will need a longer distance (more contacts) to spread to any other node. Eventually, if enough local bridges are deleted, bridges start being deleted and this will result in the above scenario where we’ll have smaller components.
I enjoyed how we could apply the knowledge of graph theory to actual contact tracing and actually apply the theory in explaining why it would work, and I found it fascinating that even on a fairly basic level without going into too much detail, we could find connections between course work and current events. I look forward to learning more about the network of contagions and epidemics later in the course and see how we can contrast that with what I have put here so far.