When Google created founders Sergey Brin and Larry Page created the RageRank algorithm in 1998, I doubt they realized how many applications it would have, and that one of those applications would be playing Tetris! In this blog post, I will analyze how Artificial Intelligence and PageRank can used to play a near perfect game of Tetris.
In Tetris, the goal is to stack pieces on top of each other without reaching the top of the board, where each piece is four blocks connected together. You can clear lines by filling an entire row of spaces, where each row is ten blocks long. A common strategy is filling a nine by four space with pieces, then using a one by four piece to clear four lines at once. This is called a Tetris.

We can use PageRank to build efficiently build a nine by four stack with no holes. With this, we can continuously create the opportunity for Tetris’ regardless of the order of pieces we are given. First, we define our nodes and edges. Our nodes are the contours of the stack. Each stack surface is represented a list of numbers in between -4 and 4, where each number is the change in height between columns in the stack.
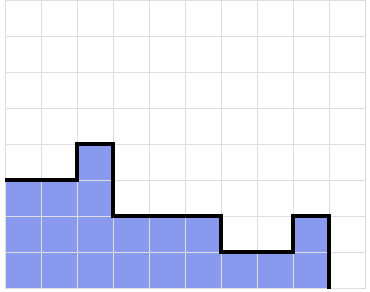
Currently, the list of numbers representing this stack is 0, 1, -2, 0, 0, -1, 0, and 1. This can be represented as a positive integer value, with each number in the set incremented by four. Thus, this surface contour is represented as a node with the identification number 45244345. If adding a piece to a surface contour A will create a new surface contour B without creating any holes in the stack, then we say that node A points to node B.
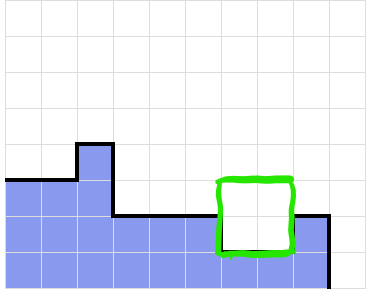
If a piece was added to this position, node 45244345 would link to node 45244543. With this, given a surface and a new piece, we can calculate all the new possible surfaces by simulating all possible piece placements that do not create a hole in the stack. We then record the results of this simulation as a graph. Finally, with this new graph, we iteratively calculate the rank of each surface following the PageRank algorithm.
When playing Tetris, players are given a random piece. Using this piece and the players current surface, we place the piece in the position that forms the surface contour with the highest page rank. Following this, we continuously stack pieces in nine by four fashion until we reach a certain height in the stack. When this height is reached, we use a one by four piece to create a Tetris, clearing four lines and lowering our stack.
This works because the only way to lose at Tetris is to have your stack touch the top of the board. For this to happen, you must be unable to clear any lines, and for a line to be unclearable, there must be a hole in the stack that gets covered by another piece. In our page ranking algorithm, a node’s rank corresponds to how likely the stack it represents is to not lead to stack contours with holes in future moves. By this logic, following the highest page ranks minimizes the likeliness of creating holes in the stack. Therefore, we can be sure the moves that are being made result in the smallest chance of losing.
Sometimes in Tetris, players are given a “next” bar, that shows the next upcoming pieces that are going to be given to the player. With this added information, we can “look ahead” and find the highest page rank along a path as opposed to the highest page rank across just one link. It turns out that having this extra look ahead drastically changes the number average consecutive moves where no holes are made.

I think using PageRank in this way is interesting because it is a unique and creative way to play a game. The fact that PageRank can be used this way is astounding because it shows an application of the algorithm outside of data analysis. Another byproduct of this is that by analyzing the weight of the links created with the PageRank algorithm, we mathematically define that some orientations are better than others, and that each piece has an optimal placement when given a stack contour. The author created some guidelines to follow to achieve optimal piece placement during a game of Tetris, which is linked to below. I chose to write about this because I personally am avid player of Tetris, so I thought it was interesting that a PageRank algorithm could apply to the game. Finally, this relates the class material because we are learning about PageRank in class. This article also forces the reader to think deeper about the implications of a node having a high rank.
Sources:
https://www.ryanheise.com/tetris/tetris_artificial_intelligence.html
https://www.ryanheise.com/tetris/tetris_stacking.html