Game Theory and Presidential Elections

Now that the 2020 US presidential elections are on the verge of concluding (as of writing this article), the whole world awaits for the results. The fate of the candidates are decided by voters and therefore, to understand the results of an election, we need to go into the minds of the people who voted. Why did a voter pick a particular candidate over the other? What factors could have influenced their decision? What was their rationale? As we will see, presidential elections are nothing more than just a game (a rather complex one). However, in principle, it is very simple. We will make use of a much simplified version of the elections to understand this very principle, employing the use of game theory to dig into the minds of the voters.

In the “toy” election we are about to study, we have 5 voters from A-E and 5 candidates from 1-5 such that candidate 1 and 5 are opposites in their views (democratic vs republic). We will inspect multiple “games” and see how the situation is played out in each of these “games”. There is a utility function that compares the result of each game. We study whether the Nash equilibrium is optimal for the voting system.

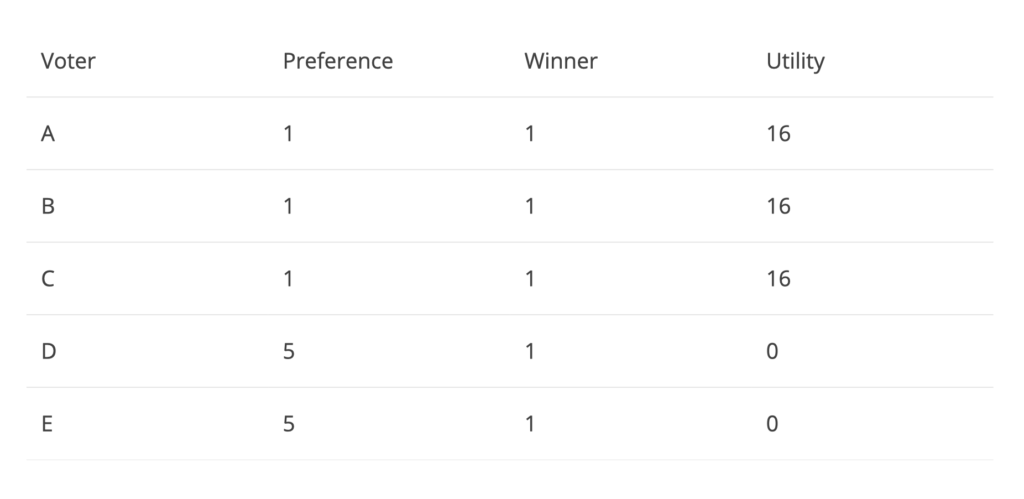
In the above game, voters A, B and C prefer candidate 1 whereas D and E prefer for 5. In this situation, Nash equilibrium will be achieved only if the voters have no incentive to deviate from their preferential candidate and hence each voter will vote for their preferred candidate. We can see that since voters A, B and C voted for the winner of the elections, 1, their utility can be said as 16 whereas D and E had no utility since they strongly voted against 1 and instead of the other side of the spectrum by voting for 5. The total utility is 48 for the above example. Let’s see if we can improve this result of Nash equilibrium.

In the above situation, somehow the winner is 3 even though none of voters A-E voted for 3. Candidate 3 can be thought of as a neutral candidate which is not strongly disliked nor strongly liked by voters A-E. The total utility of this game is 60. We can see that the outcome overall, is better the in Figure 1 even though the winner was a candidate not the preferred candidate for any of the voters. The above example explains how voters cannot predict how others will vote and hence, they simply pick whichever candidate they prefer the most, even if the result is not optimal. Now let’s consider another game:

This situation is similar to the one in figure 1 with a utility of 51. This time, we will follow this up with the next elections (4 years later) where the voters can see the results from the previous elections. Voter D prefers 5 over 4 and can switch his vote over to 5 during the next elections. Hence, it all comes down to the neutral voter C. He/she neither strongly likes nor strongly dislikes candidates 1 and 5. C can simply “throw away” their vote to either 1 or 5 and can be indifferent to the outcome of the election. Say C throws his/her vote to E. Then in that situation, we can observe the following:

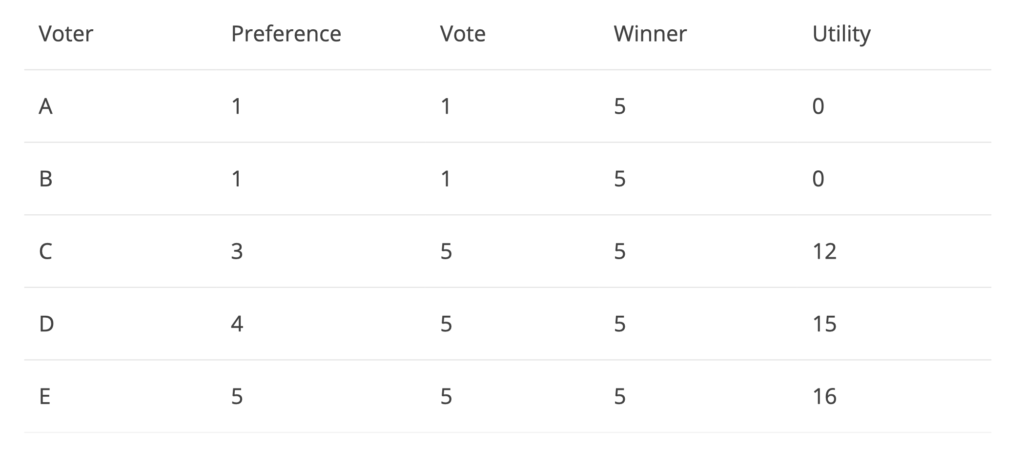
Since voters A and B Strongly dislike the winner – candidate 5 and hence vote against 5, they have no utility. Notice how C votes for 3 even though he/she prefers 3. Since the previous round of elections showed that 1 and 5 are the main polarizing candidates, C would like to have some representation over no representation at all by voting for one of the two polarizing candidates. Calculating the utility of the above game results to 43, which is worse than what we obtained in figure 1!

Looking at the games above, sometimes voters A and E are extremely satisfied with the results whereas sometimes they are extremely dissatisfied, producing suboptimal results. If voters such as C did not swing to either end of the spectrum to have some kind of “representation” (1 or 5), they could remain in moderate and hence resulting in an optimal election outcomes as in Figure 2. The government needs to modify their election system to switch to a better one where the results are moderate and produce the most optimal results. Otherwise, the country will be left in a situation where some citizens strongly dislike the president and some strongly like the president, which has been the state of the US over the past 4 years.

Reference:

Disastrous Elections: Predicted by Game Theory