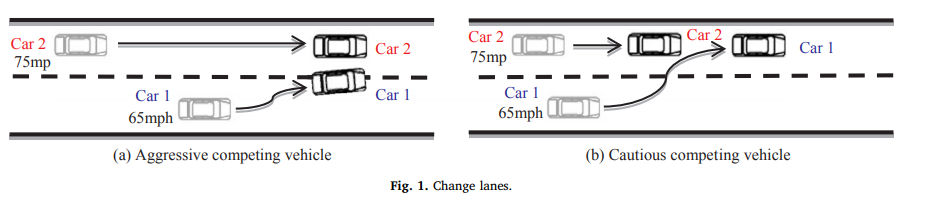
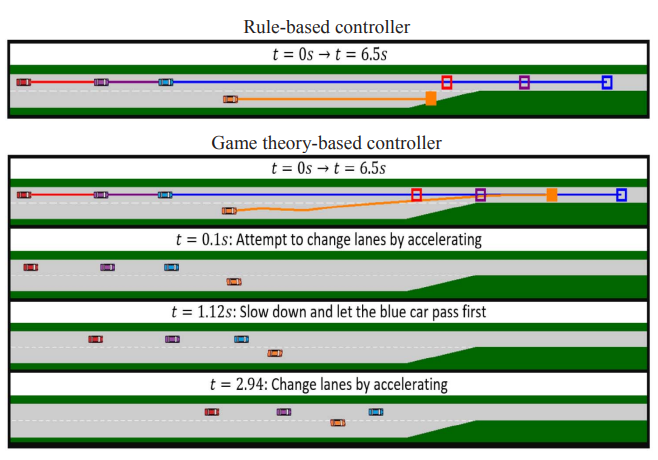
In self driving cars and autonomous vehicles, one of the most important features to implement to make a truly self driving autonomous car in a environment where there are a mix of both self driving and manually driven cars is lane changing. In a lane change, the autonomous vehicle has to predict the actions of the vehicles in the incoming lane and adjust speed and decide on when to commit to the merge. This decision is one that needs to be made before the merge lane ends and is subject to a lot of adjustments and on the fly decisions. An aggressive approach can be potentially dangerous and a cautious approach might impede traffic.
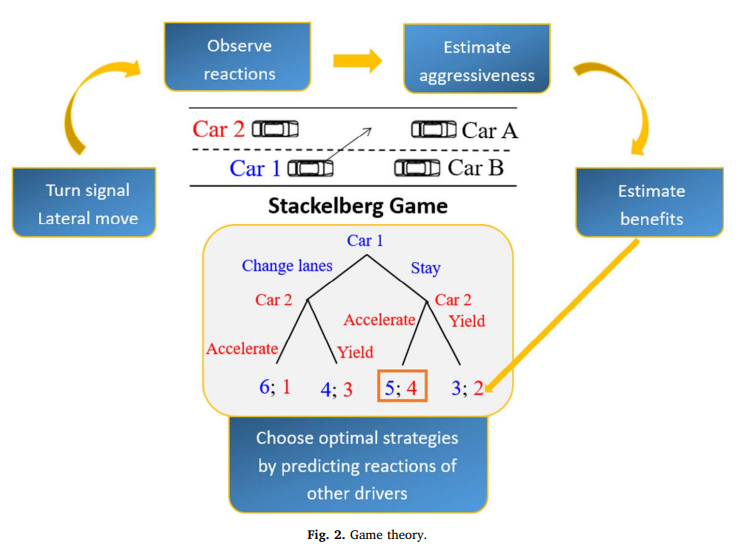
This decision and control can be modeled as a game, in which the payoff is a compilation of several factors, the safety, which is calculated by the rate of change in the safety factor between the time the decision is calculated and the moment, and the safety factor is calculated by the distance between cars as defined by this function:
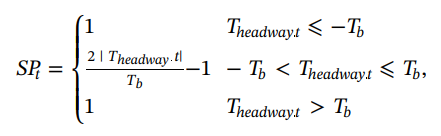
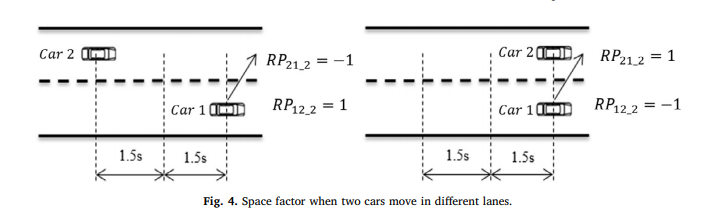
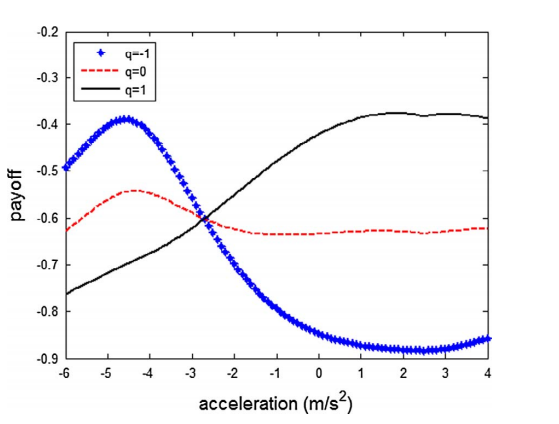
The payoff also factors in the distance between the two vehicles, this payoff also takes into account the time it takes for the vehicle to merge into the destination lane.
The total payoff is a linear combination of the two above payoffs.
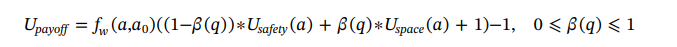
And the payout function can be estimated given the parameters fed to it by the car:
And the game can be solved by the equation:
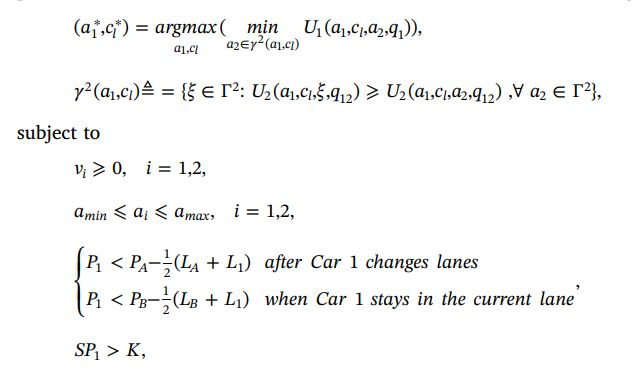
where Ut denotes the total payoff.
The article then breaks down the lane merging action into a game between two cars. And the payoff of the opposing car can be estimated by the aggressiveness estimate, can let the merging car predict to a extent the behavior car 2 will take.
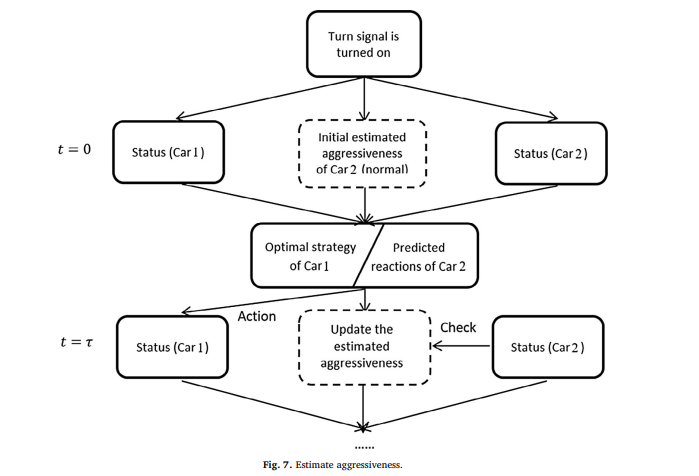
Citations:
Yu, H., Tseng, H. E., & Langari, R. (2018). A human-like game theory-based controller for automatic lane changing. Transportation Research Part C: Emerging Technologies, 88(Complete), 140–158. https://doi.org/10.1016/j.trc.2018.01.016