The fresh water supply in the world is limited and its demand applies to everyone. We use fresh water for agriculture and food production, which in turn helps provide sustainability for our living conditions. What would happen if countries were to fight for fresh water? We can investigate through game theory by creating game models to demonstrate how a country would act in accordance with other countries.
In the game model, we have two players and their strategies will be limited to two. What the strategies are will depend on the situation presented. We’ll see how the game models operate similarly to previously seen game models such as Prisoner’s Dilemma.
In an intra-country example, we consider two farmers extracting water for their crops. They are offered the choice of two aquifers, where the first aquifer has a lower pumping rate but lasts longer, while the second aquifer has a higher pumping rate but lasts shorter. There are only two aquifers, so in the case that both farmers choose the same aquifer, they must share it. Figure 1 shows the payoff matrix demonstrating each player’s utility in each scenario.
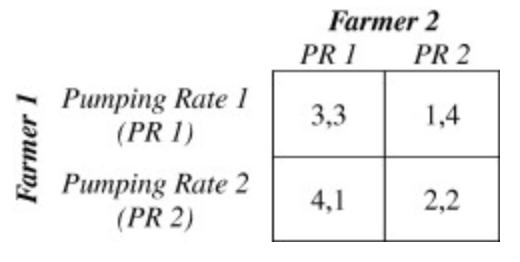
Here we see the familiar Prisoner’s Dilemma game model, where the dominant strategy for both players is the second strategy, even though the optimal cooperative outcome is the first strategy. This represents the real-world scenario where two parties can slowly share a water resource without depleting it versus quickly share a water resource and emptying it.
Another instance where game theory can be applied is the Iran-Afghanistan Conflict, where both Iran and Afghanistan depend on the Hirmand River for their agricultural needs. However the river must be maintained to sustain itself, so one or both of the countries must expend some cost to fix up the river. Here the strategies offered are to pay or not pay. Figure 2 shows the payoff matrix of such a game model.
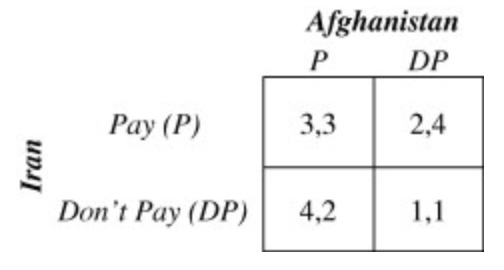
Here we see there’s no strictly dominant strategy, however, we are able to establish two pure-strategy equilibria. These two equilibria involve the case where one country pays while the other does not, which correspond to (DP, P) and (P, DP). Intuitively, the country not paying gains the most amount of utility since they can enjoy the river while not sacrificing any costs. Furthermore, the country paying the cost may not receive as much utility but having access to the river is evidently better than not having access. There also exists a mixed-strategy equilibrium where both players choose to pay with p=1/2, which yields an expected payoff of 2.5. This scenario of the two countries show how water resources can benefit both parties, but only one might try to maintain the water resource.
These two game models do not show the full story, since if one country was more fortunate than another country, their utility payoffs can differ. For instance, if it was Canada and Iran as the players, Canada may have a higher payoff even if they were to pay the costs. This is because the costs can be viewed as negligible.
In conclusion, with fresh water resources being essential to agriculture, game theory has proposed some strategies countries can take. This will depend on the countries’ fortunateness and whether they adapt a cooperative or a non-cooperative stance.
References:
- https://www.sciencedirect.com/science/article/pii/S0022169409007653
- https://www.bbc.com/future/article/20170412-is-the-world-running-out-of-fresh-water