Idealized Analysis of Social Networks in ORGs

[This blog post can serve as continuation of my previous post, though it has enough original content to stand on its own.]

[tl;dr? Go and play around with Big Brother Bots on my website now!]

What is an ORG?

If you have read my last blog post, you can skip this section. ORGs are Online Reality Games. They take place on private online forums in which players can send private messages to each other, compete in online challenges, and cast votes to eliminate one another until a winner is declared. Every 48-72 hours, one or more players are voted out of the game. Games typically last 40-60 days. Throughout the course of the game, players are divided among many different subgroups (tribes). Communication is only allowed among members of the same tribe at any given time. Eventually (usually around 13-11 remaining), the tribes all merge into one tribe and remain that way until the game ends. At the end of the game, two players remain, and a jury of recently eliminated players vote on who they think the winner should be.

It is also possible to sign up as a spectator, meaning you would have access to all the boards of the game. As a spectator, one does not have access to the private messages that players sent to each other, but they do have access to private “confessional” subforums for each player, in which players were encouraged to post their thoughts and plans for the game.

Going Beyond the Data

In my last blog post, I demonstrated a new interface for visualizing social networks in online reality games, and analyzed what it did well, and what it did poorly. I also discussed some of the limitations of gathering real data from such games, namely that players are not guaranteed to volunteer complete or accurate information, due to the stress and complexity of the game being played.

Because of these limitations, the resulting interface I created ended up not being a tool that visualized the social network, but rather a tool that visualized an approximation of the social network. This observation naturally leads to the question: What would a tool to visualize the actual network of the game look like?

Introducing Big Brother Bots

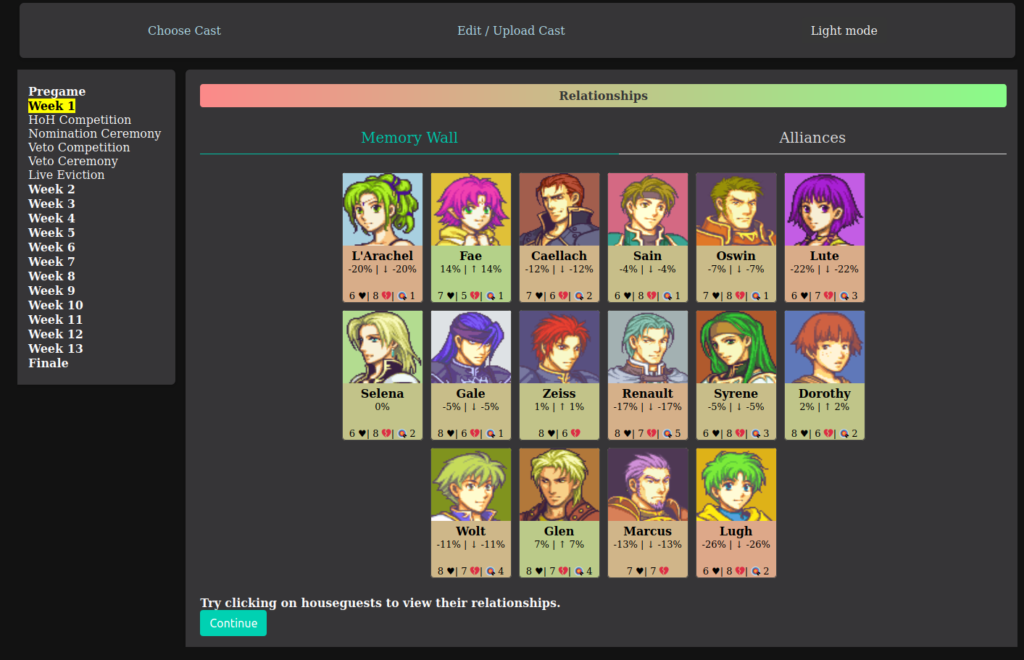
In order to further look into this problem, I created the webtoy Big Brother Bots, or BB-bots for short. Big Brother is a game in which players compete in challenges for power in the game, and eliminate each other one by one by majority vote. When only two players remain, a jury of previously eliminated players vote on who they want to see win. Each round (Week) of Big Brother is split up into 5 phases. In the Head of Household competition, a player is randomly selected to win Head of Household. The same player cannot win this competition twice in a row, unless there are only 3 players remaining.

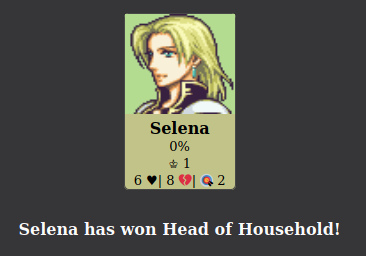
The Head of Household (HoH) will then nominate two players for eviction. Players nominated for eviction are at risk being voted off.

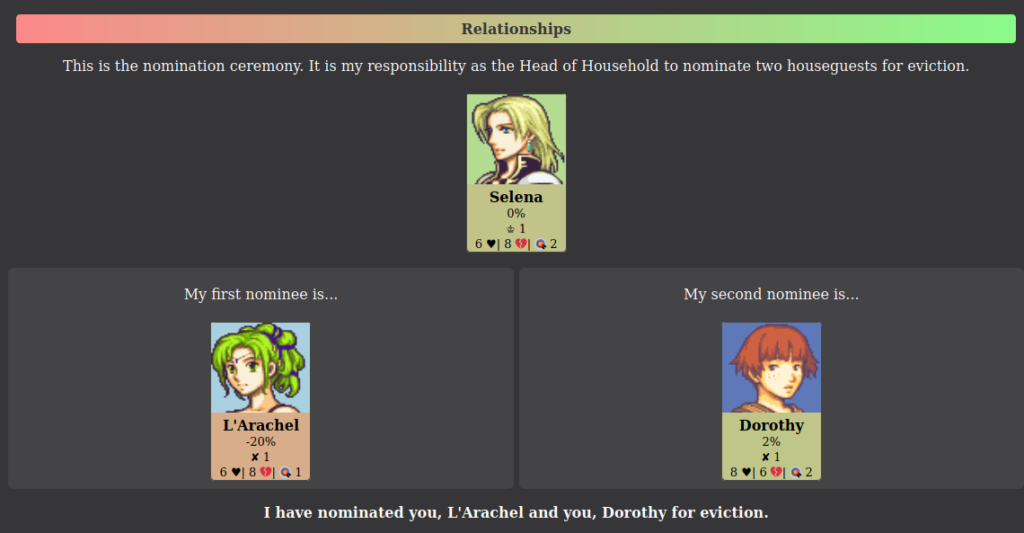
The players nominated for eviction will have a chance to save themselves by playing in the Power of Veto competition. The Head of Household, the two nominees, and three other random players will have an opportunity to win the Power of Veto (PoV), which enables them to veto one of the nominees. They can also choose not to use this power. In the game, the winner is chosen randomly.

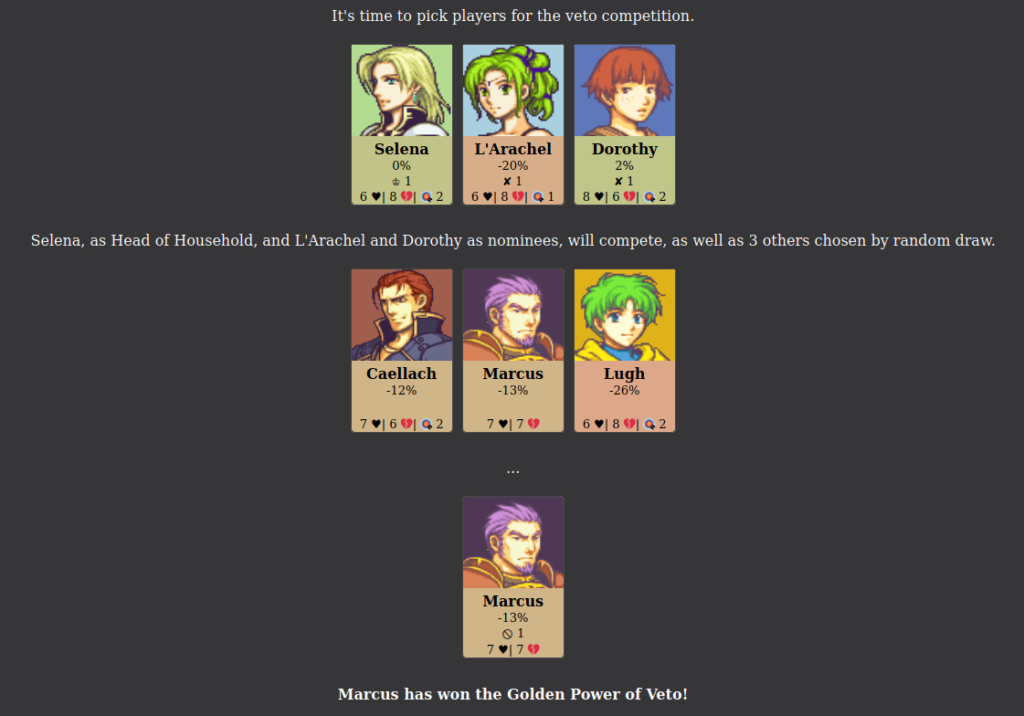
If the power of veto is used, the Head of Household must name a replacement nominee. The winner of the Power of Veto cannot be named as a replacement.

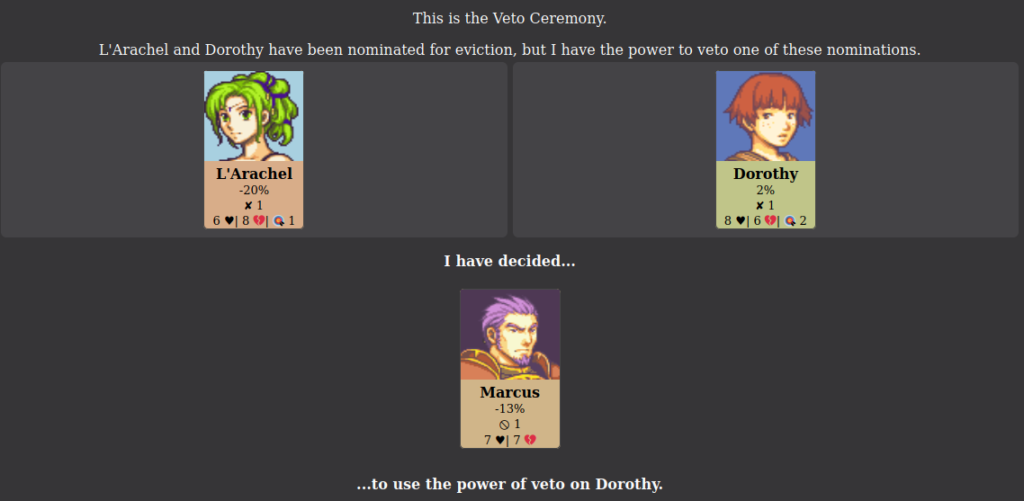
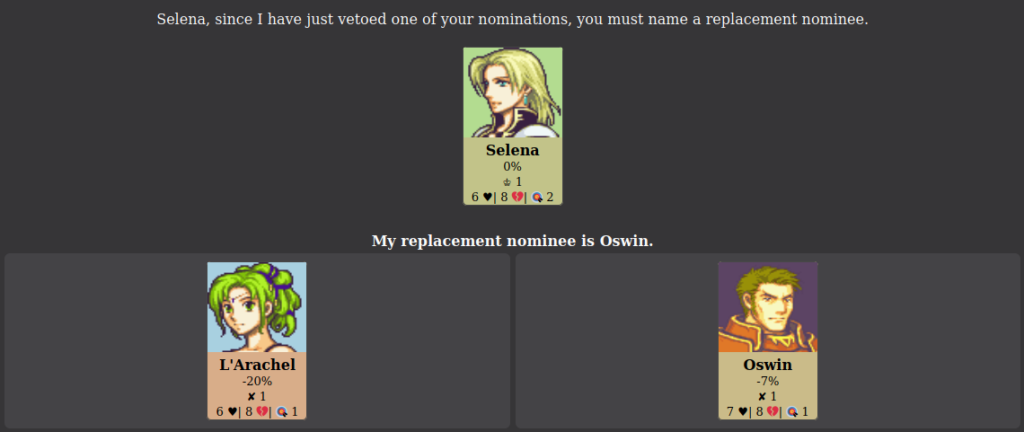
At this point, all the players in the game, except for the Head of Household and the nominees will cast votes on which of the two nominees they want to see eliminated from the game. The Head of Household only votes in the case that they need to act as a tiebreaker.

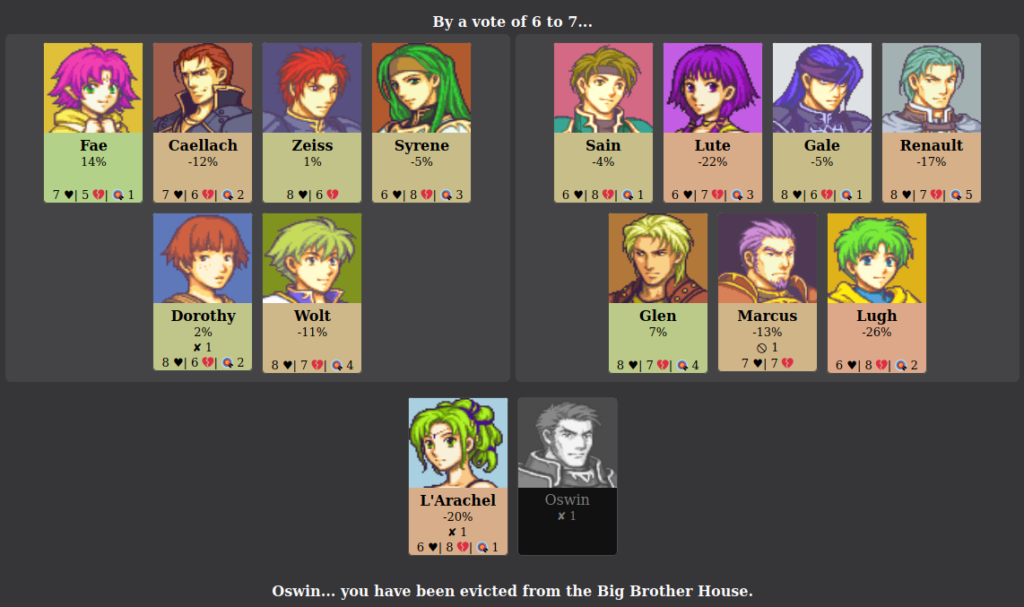
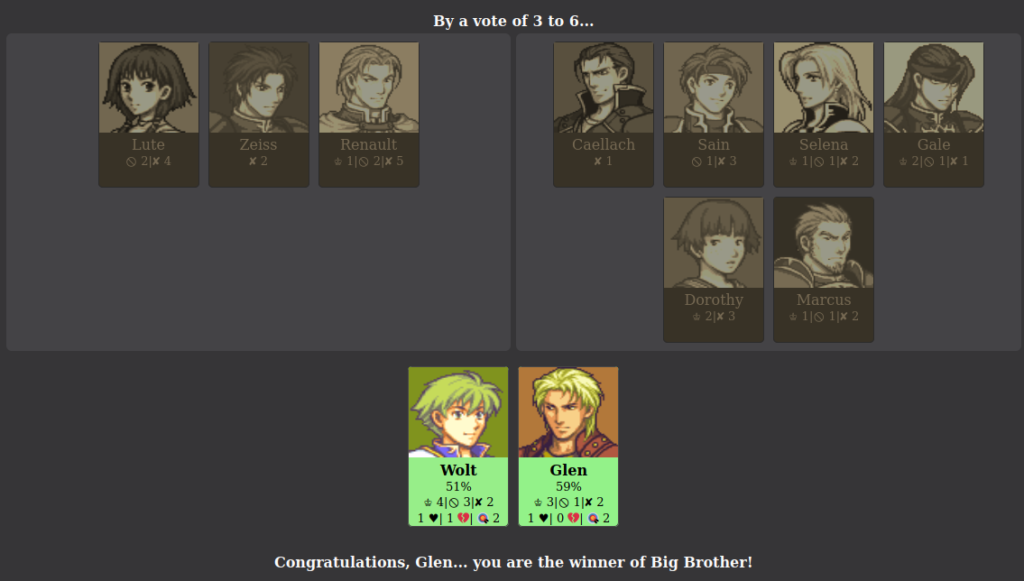
This repeats until only two players remain, at which point a jury of recently eliminated players votes on a winner.

Social Network Model

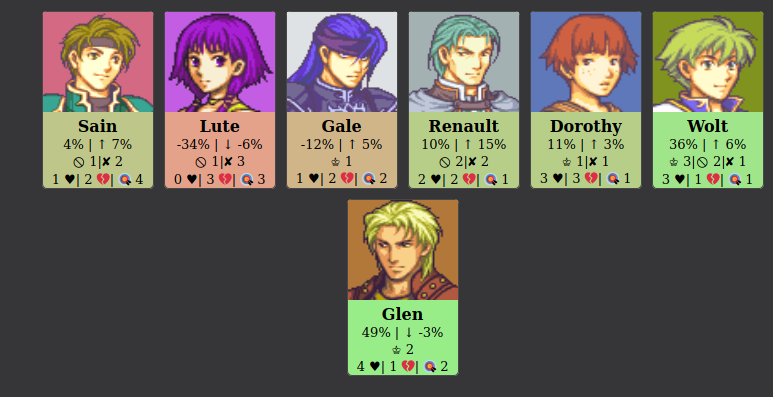
The model for the relationships in the social network is a complete undirected graph with edges of uniform random weight in between -1 and 1. This is then displayed as a number between -100% and 100%, and does not change throughout the game. The little cards generated for each player contain a lot of densely packed information. Here is a summary:

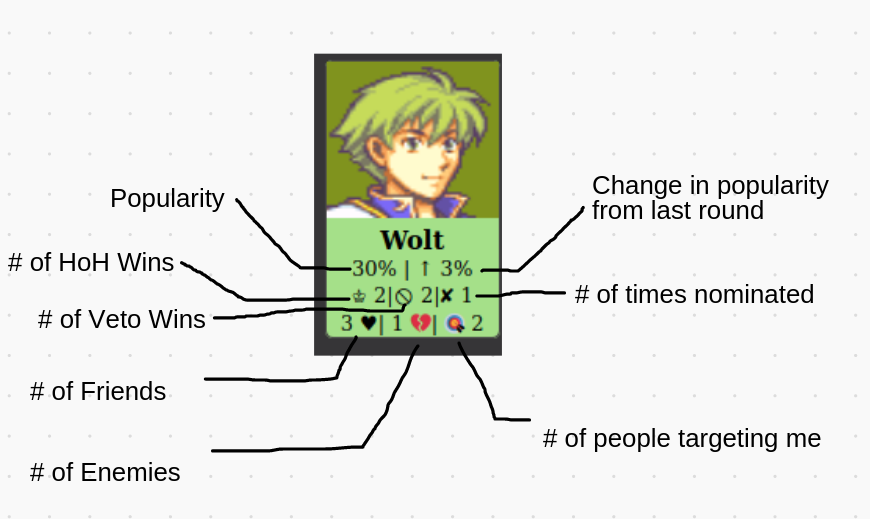
Popularity is the average of a player’s relationships, and dictates the background colour of the card. This gives an immediate visual indicator of generally how well liked a player is. HoH/PoV/Nomination counters are self explanatory and not related to networks. The number next to the target emoji counts the number of players in the game that would nominate Wolt this round if they won Head of Household. This gives a good indicator of how much danger a player is in. Friends and Enemies are calculated in a different way.

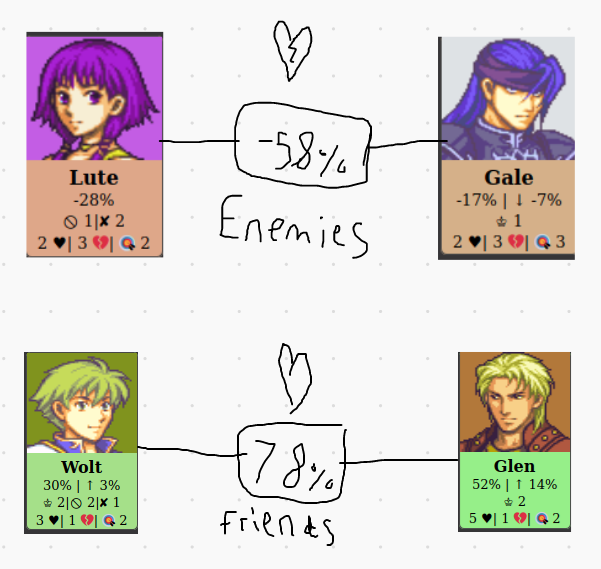
Friends and Enemies are relative to a player’s popularity. If the relationship between two players is less than each of their popularities (ie. worse than average), they will be enemies. If the relationship between two players is greater than both of their popularities (ie. better than average), they will be friends. The intuition being that a friend is someone you treats you better than average, and an enemy treats you worse than average. It is also possible for there to be a one-sided relationship, which is called the pawn/queen relationship (named after chess).

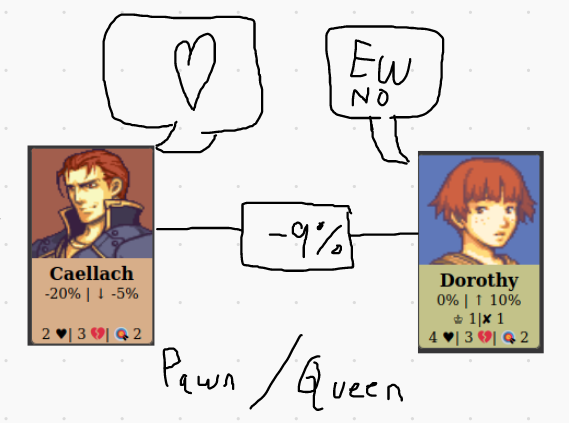
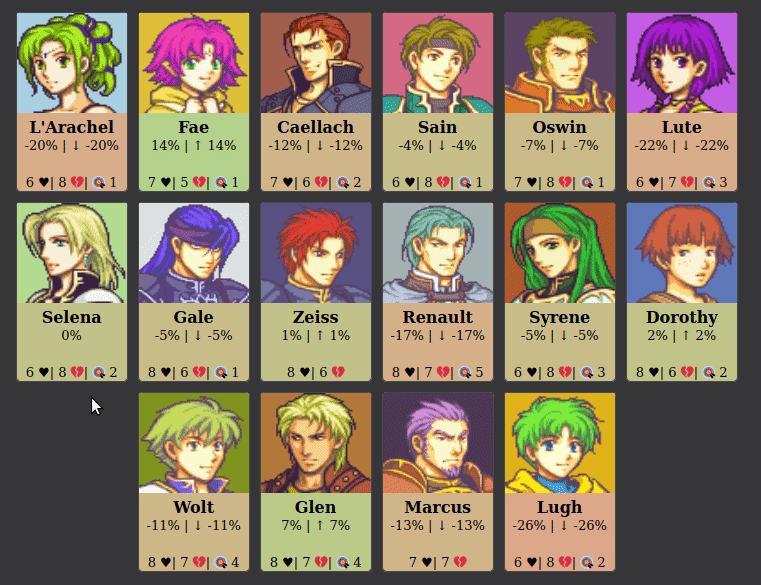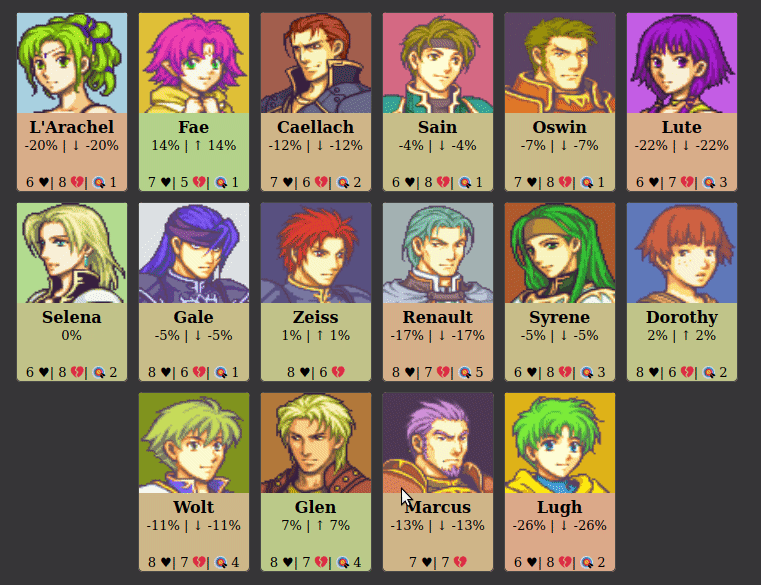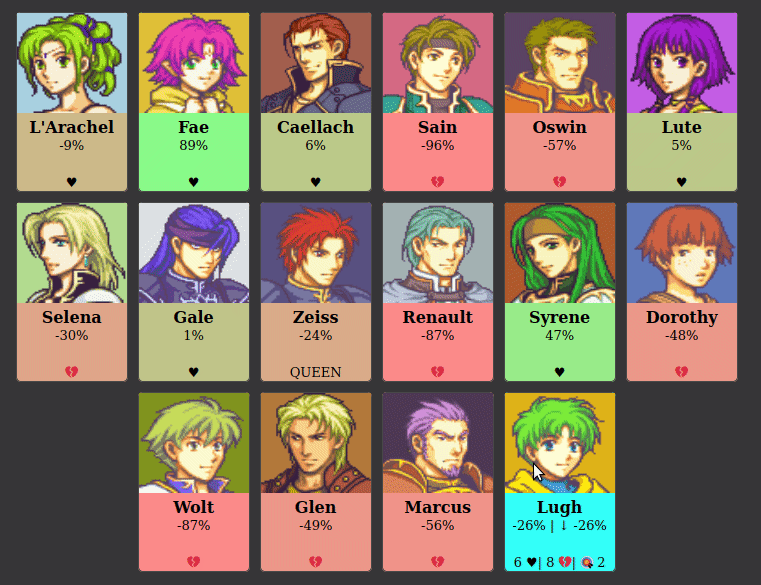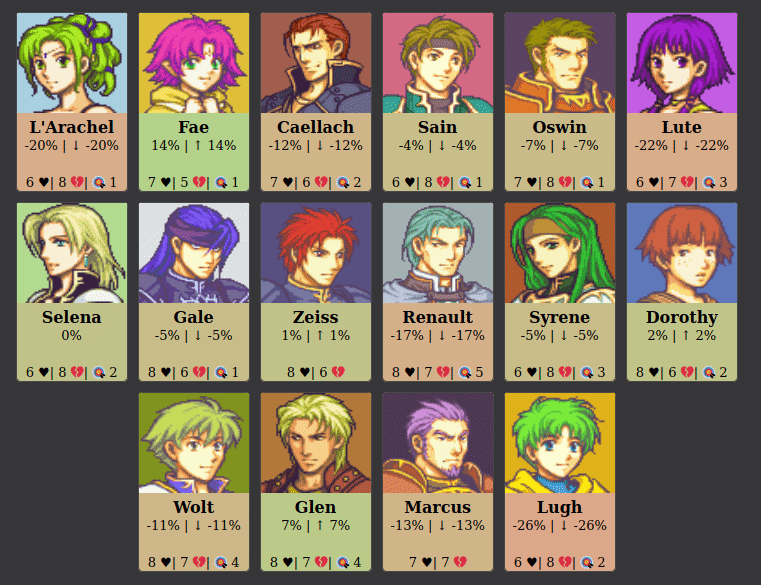
In this example, Caellach’s relationship with Dorothy is better than average for him, but Dorothy’s relationship is worse than average for her. This leads to a one-sided relationship between the two of them.

One may wonder why it is necessary to have relationships be tied to popularity. The reasoning for this is thus. Big Brother is a game that ends with only one winner. If six players formed a coalition and successfully eliminated every other opponent, they will be forced to turn on each other when there are six players remaining. At this point, a coalition of six makes no sense anymore, since every coalition, by nature of the game requires a common enemy. The nature of this model is that as enemies are eliminated, weak friendships break down, and as friends are eliminated, weak enemies put aside their differences. Behold an example from the game:

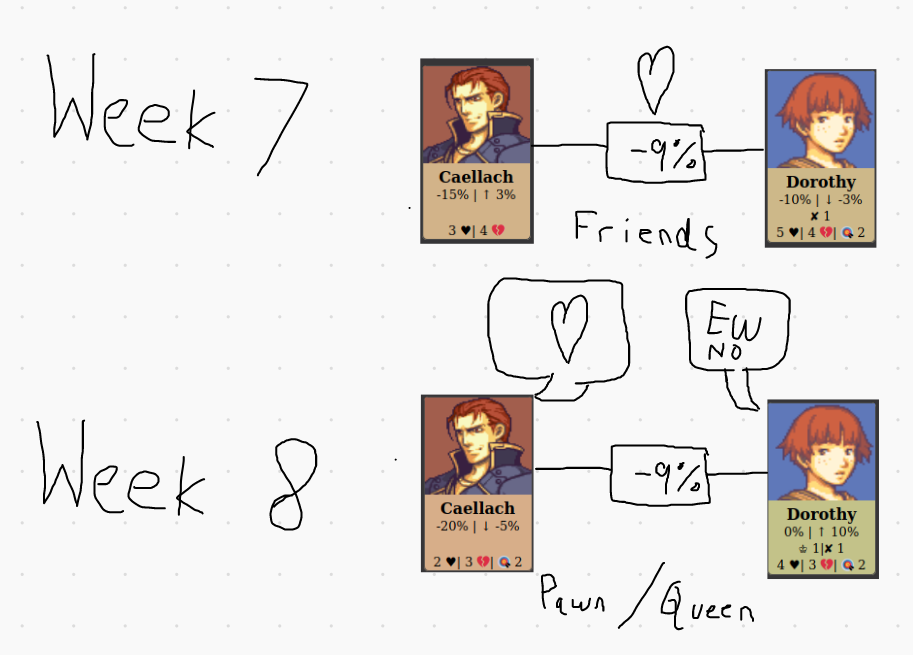
Between Week 7 and Week 8 of the game, Dorothy’s enemy Selena is evicted. Since the relationship between Dorothy and Selena was very extreme (-86%), Dorothy’s popularity was skewed downwards. Once Selena is gone, Dorothy’s popularity goes above -9%, and her relationship with Caellach becomes one-sided.

Criticism of the Social Network Model

This is not a realistic model of a social network. It should be quite easy to come to this conclusion based on the fact that all the relationships are uniform randomly generated between -1 and 1. Real social networks, as seen in class, tend to have clustering and communities. Comparing the random data from this model to the real data from the game I spectated confirms this hypothesis.

It is also worth noting that due to the “winner take all” nature of ORGs, the properties of real data from these networks does not necessarily match the properties of real data from real social networks. This is discussed in a different post, but it is worth bringing up again as a segue into the next topic.

A Game Within a Social Network

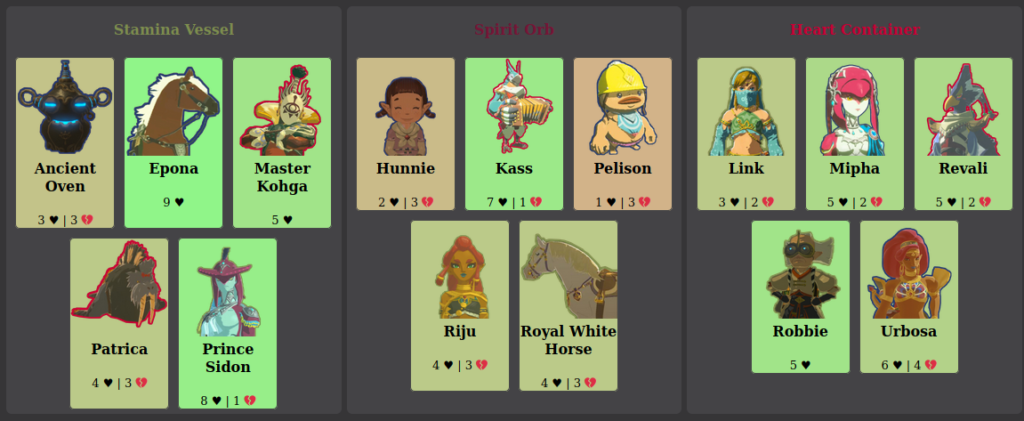
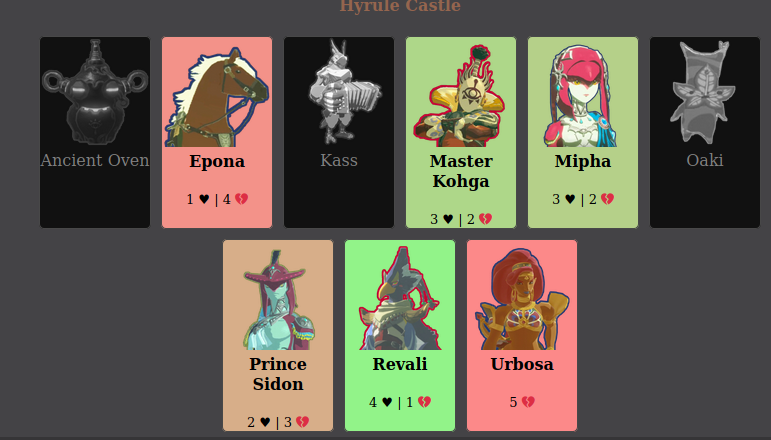
As the name might suggest, an Online Reality Game is a game. While the nature of the game encourages the building of social relationships, the win condition of Big Brother is to be one of the last two players standing, and convince a majority of the jury members to vote for you as the winner. And not all players are created equally. It is an observed phenomenon in past reality shows of the same nature [Big Brother 22 Spoiler] that players that had a lot of positive social connections are more likely to win over the jury at the end of the game. Sometimes, players will realize this, and backstab their more socially connected opponents as it gets close to the end of the game. I was able to observe this exact phenomenon in my real data, in which the best connected players early on (Kass, Epona, Prince Sidon) all had their connections rot away near the end of the game, where they were voted out in 8th, 6th, and 5th place respectively.

Players can deduce who they have a better shot at beating in the finals, so they try to get to the end with these people. They also know who would beat them in the finals, so they work to take these people out before it gets too late.

Jury in Big Brother Bots

The algorithm for deciding a jury vote in BB-Bots is very simple. Each juror votes for the finalist they have a better relationship with. This mirrors the observation that more connected players have a higher chance of winning at the end of the game. Since relationships in the game don’t change, it is easy to compute the results of every single possible finale and display the results to the user. This metric is referred to as Power Rankings.

A clever observer will realize that this is a special form of a graph, called a tournament. Every matchup of two players has a winner and a loser, so a directed graph can be constructed by drawing from the winner to the loser in every matchup.

The introduction of this structure dictating who wins the game presents an interesting dilemma for players. Wolt will beat everyone except for Glen, so he needs to vote out Glen sometime before the end of the game. But if Wolt votes out Glen, everyone left in the game loses to him, and thus, he risks being voted out next. Gale is on the other end of the spectrum, where his only win condition is to get to the end of the game with Lute, but can vote out anyone else in any order.

It is a bit easier to understand see the ideas behind this game when the tournament is transitive. Lute is voted out next, and the game looks like this:

Since Gale no longer has a chance of winning the game, he instead makes decisions entirely based on relationships, opting to vote off his enemies and protect his friends. Glen also plays entirely based on relationships, since he too is indifferent of who he goes to the end of the game with, the difference between them being that Glen always wins and Gale always loses. This “blog post” is already almost two thousand words long, so I will leave some questions as an exercise to the reader. Can any two players in the above game form a coalition where neither of them have incentive to betray each other? Can any three players in this game form a coalition intending to eliminate the other two first, where none of them have incentive to betray each other? Since relationships are not given, you can assume them to be anything you like in order to satisfy these conditions. Just make sure to state what you are assuming the relationships to be. I look forwards to the comments this will surely receive.

Criticism of the Jury Model

While this model does a decent job of imitating reality, an observer of a game may complain that it is uninteresting to see a player who has zero chance of winning be allowed to remain in the game. This can be partially remedied by changing the way the jury votes work. Instead of having the jury votes be given out deterministically to the finalist with the highest relationship, perhaps instead the juror will simply be *more likely* to vote for the finalist they have a better relationship with: with the exact probability being determined by the difference in their relationship with the finalists. This may still lead to a scenario in which one player has zero chance of winning. How this might be possible is left as an exercise to the reader.

Conclusions

By creating a simple model of an ORG social network, it is possible to learn more about ORG social networks and gain insights about how they can better be analyzed and understood. Even with unrealistic relationship data, the nature of power rankings data can be better understood.

My next goals in this project are as follows: First, to implement the non-deterministic jury vote algorithm described earlier in the post. Then, to make relationships more realistic, and use a model that can dynamically change and meet clustering and community requirements expected of an ORG social network as the game shrinks. I predict that further options for visualizing the structure of the network will open up once the social network generator is conforming to a realistic model.

Links:

My previous blog post [Contains more information about real data]

Big Brother Bots [Try playing for yourself!]

Project-LSG [Explorer/source for the real data seen above]