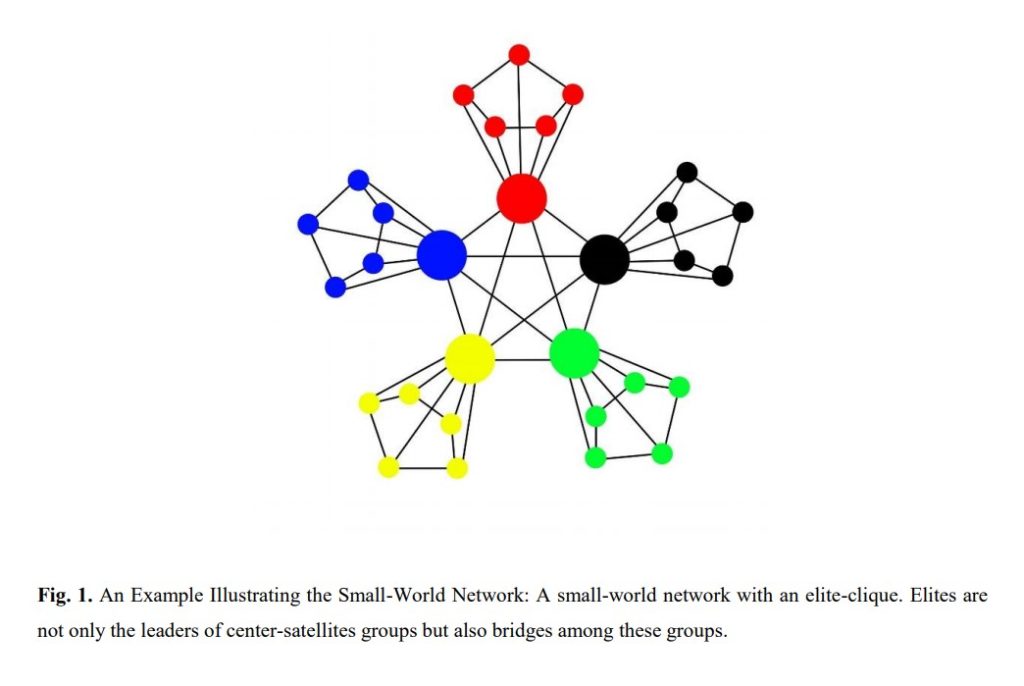
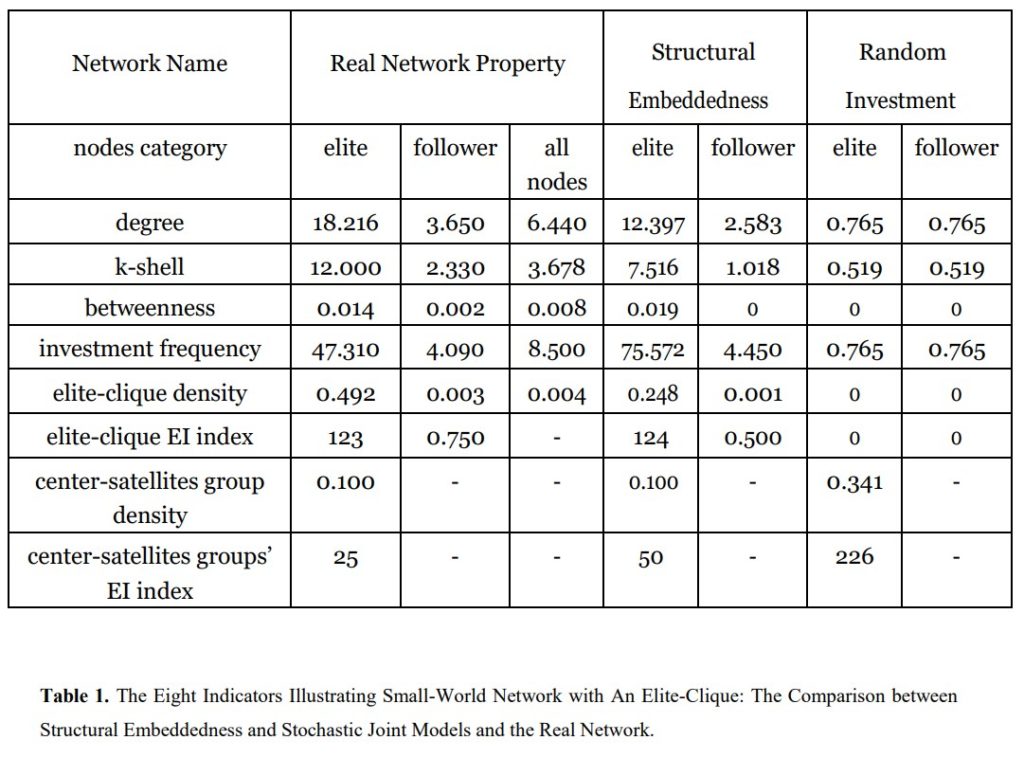
When discussing game theory, it’s easy to forget its applications beyond just games, as the name would deceptively suggest. The mathematical field of game theory can provide elegant ways to strategize very real and difficult problems. When I was reading the blog post titled ‘Coordination Failure’ by Linda, I found the mention of the nuclear arms race most fascinating. This was also briefly brought up in the blog post titled ‘Balance of Top Countries, A View of Their Relationship Network’ by Jiale. This prompted me to do more research and further uncover how game theory can be applied to arguably one of the most serious and/or dangerous situations we face as a society.
I came across an analytical article from The Washington Post called ‘What game theory tells us about nuclear war with North Korea’ by Elizabeth Winkler. This article was written in August of 2017, when tensions between the United States and North Korea were seemingly at all time highs, with a looming threat of nuclear war. Something interesting that was pointed out in the article is that the use of game theory for military strategizing is not a new concept. In fact, it seems like we’ve done it ever since the theory itself was formalized! We’ve seen in class that what may be independently best for the players, which is what game theory aims to model, may not always be the best choice overall, which is personally a little scary considering that’s the difference between nuclear fallout and not in this case.
The article, which is actually framed as an interview between Winkler and Stanford professor Tim Roughgarden, draws parallels between nuclear strategy and the Prisoner’s Dilemma that we’ve also seen in class.
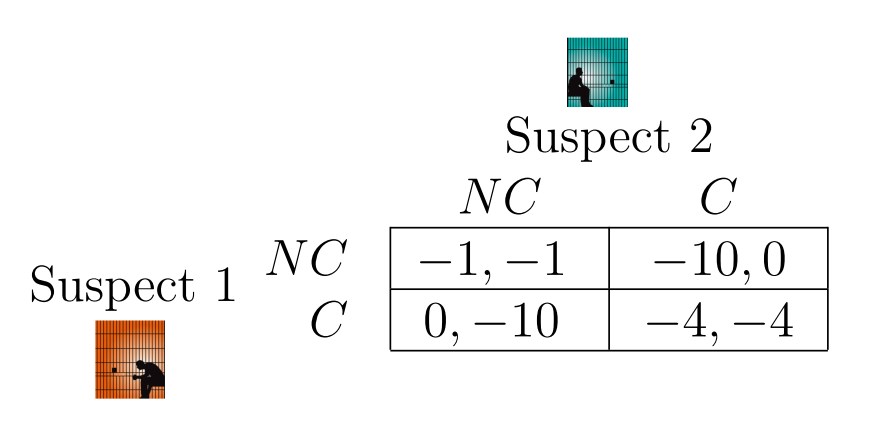
In the Prisoner’s dilemma, the two “players” are suspects in custody who either have the option of confessing to a crime or not. Their payoff (or punishment rather) is not only dependent on what they choose to do, but also what the other suspect chooses to do. Roughgarden claims this is analogous to the United States and the Soviet Union during the Cold War. In that scenario, the (simplified) options were to either attack with nuclear weapons or not for both countries. A similar payoff matrix could be determined for the Cold War using arbitrary payoff for winning or losing:
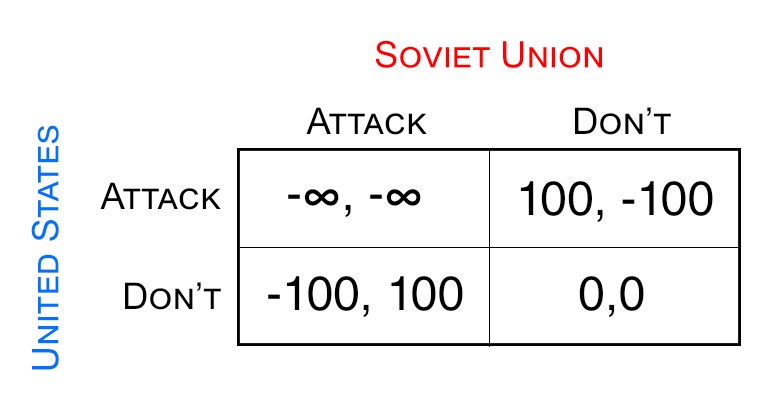
There are a few differences between the Cold War era and the North Korean era. First of all, during the Cold War era, both the US and Soviet Union were neck-and-neck in terms of their capabilities to wage war. This meant that the “game” was balanced in which both players had roughly equal actions. From a game theory standpoint, this is ideal. However, naïve analyses like this are flawed in that they don’t take into account repeated games. For example, it’s likely in a country’s best interest to attack, but this can cause other parties to behave differently in the future. The article mentions that the conflict between US and North Korea is almost a second round or repeated “game” of the US and Soviet Union one.
When asked what action the US should take, Roughgarden refers to an example that we’ve seen in class where two people would prefer to go to dinner together, but have different food preferences. This idea of multiple Nash equilibria where there are multiple best options isn’t clear from the payoff matrix above, but that’s because of another flaw of applying game theory to analyze war strategy. Roughgarden says that it’s simply not clear what the other side will do or how rational they may behave. We know from class that the models we have learned require the assumption of equally rational parties. But people are people and it’s never as simple as that. Personally, this gets me more excited than ever to learn about how more advanced game theories account for unbalanced players with better accuracy.
References
Winkler, Elizabeth. “Analysis | What Game Theory Tells Us about Nuclear War with North Korea.” The Washington Post, WP Company, 29 Apr. 2019, www.washingtonpost.com/news/wonk/wp/2017/08/16/what-game-theory-tells-us-about-nuclear-war-with-north-korea/.
Linda. “Coordination Failure.” CSCC46 2020 Course Blog, 13 Nov. 2020, cmsweb.utsc.utoronto.ca/c46blog-f20/2020/11/13/coordination-failure/.
Yang, Jiale. “Balance of Top Countries, A View of Their Relationship Network.” CSCC46 2020 Course Blog, 23 Oct. 2020, cmsweb.utsc.utoronto.ca/c46blog-f20/2020/10/23/balance-of-top-countries-a-view-of-their-relationship-network/.
Anderson, Ashton. “Lecture 8.” Social and Information Networks. www.cs.toronto.edu/~ashton/cscc46/lectures/lecture8-2020.pdf.