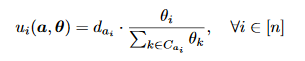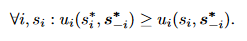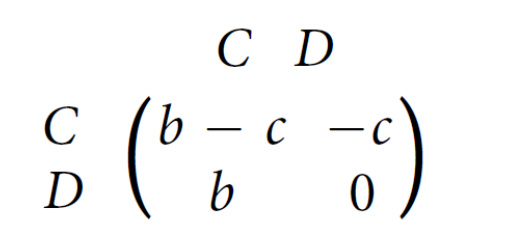In class, the prisoner’s dilemma was brought up to get an idea of how dominant strategy works. The prisoner’s dilemma has been shown to pop up in the real world, for example in arm races between countries and the overfishing problem; it’s easy to see why even though there is an optimal solution for both parties, the net result is one where both parties do worse. However, this issue is not just isolated in reality and I realized that similar social dilemma often arises in video games, specifically in multiplayer games.
The main reasons why many people play video games is to have fun, for the competition, or a little bit of both. However, even if you enjoy playing a game for fun rather than for competition, more often than not you will find winning much more enjoyable than losing. In many games, the most fun way to play will not be the most reliable to obtain a victory. This leads players to a dilemma in which they have to decide which strategy to pick that will counter the strategy picked by the opposing team. While competitive strategy can still be just as enjoyable as non-competitive strategies, there are times in games where the best strategy does not result in a fun time.
Online multiplayer game developers have the job of having to constantly patch a game even if there are no visible bugs. This is due to the fact that a multiplayer game that stays consistent and unchanged will grow stale and slowly lose its player base. To remedy this problem, developers will add new content to the game and make small adjustments that can change the meta in small or big ways. Unfortunately, sometimes the changes in the meta of the game are big and result in a less fun meta whether or not the developer intended for this. For example, “in the early days of StarCraft, a strategy called “Zerg rushing” emerged where at the beginning of the match players would quickly build lots of cheap Zerg units to overwhelm opponents before defenses could be constructed” (Madigan 2010). Before developer patches, this was the dominant and most used strategy of the game, even if it was not fun to play as or to play against. The prisoner dilemma perfectly explains why players kept using this strategy even though it was not every enjoyable.

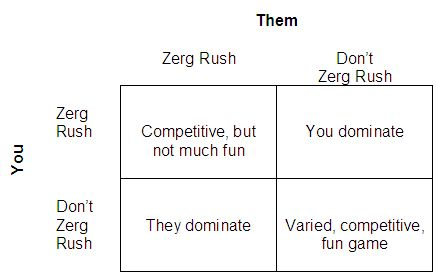
From the matrix above, one can see why Zerg rushing became so common. The dominant strategy for both sides is to Zerg rush and is a strategy that is strictly better than all other options, regardless of what other players do. While a game where neither player Zerg rushes would be ideal, if one player chooses not to Zerg rush, the other player will have more incentive to Zerg rush since they would have more enjoyment dominating the game than they would in a normal match. As a result, both players Zerg rush and the games are unsatisfying to play.
Another issue that comes from developers patching a game and adding new content is the inevitable bugs that come along with that content. Sometimes these bugs and glitches will be small and not usually have much impact on the game, but there are times when exploiting these bugs is a legitimate strategy that results in a more likely victory. For instance, “some players of the online first-person shooter Modern Warfare 2 discovered what became known as “the javelin glitch.” Someone, somewhere, somehow figured out that through a bizarre sequence of button presses you could glitch the game so that when you died in multiplayer you would self destruct and murder everyone within 30 feet, often resulting in a net gain in points” (Madigan 2010). Modern Warfare players end up in a similar dynamic as the Zerg rush problem where they have to decide which strategy will result in a more positive outcome.

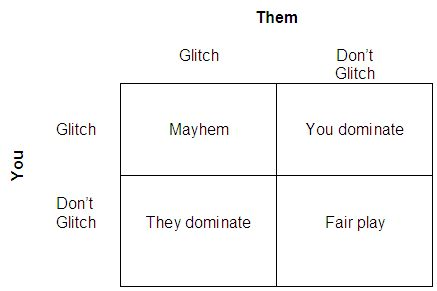
Once again, even though not exploiting the glitch would result in fair play that is optimal for both parties, instead the more common route was mayhem where all players exploited this glitch. This was so common in fact that Infinity Ward had to rush out a patch to stop it from being exploited any further. Using the same logic as the prisoner’s dilemma we can see that the dominant strategy for all players would be to glitch. The players would rather have a broken match than be dominated by opposing players.
In conclusion, the prisoner’s dilemma and game theory allow for a better understanding of social dilemmas in not just the real world, but also the virtual world. I believe that game developers at the very least can use this information to prevent players from having to be put in future dilemmas, such as by banning players that exploit bugs so that the pay off matrix will result in a dominant strategy that is fun for all players.
Sources:
Madigan, J., Says. (2013, July 30). The Glitcher’s Dilemma: Social Dilemmas in Games. Retrieved November 18, 2020, from https://www.psychologyofgames.com/2010/03/279/