At the time of writing this post, Canada’s largest sale event, Black Friday, is about 20 days away. This week, Yahoo Finance released an article called, “Your Complete Black Friday and Cyber Monday Shopping Strategy for 2020”. During the Black Friday event, consumers will be developing optimal shopping strategies to get the best deals. Additionally, retailers are constructing strategies to market and price their product to maximize their sales over their competitors. By using the material taught regarding Game Theory in CSCC46 we can understand an optimal pricing strategy in a perfect world, and how this strategy fits in an imperfect one.
Game Theory on Black Friday Pricing
In a perfect world, we may assume all entities are rotational, all entities know the rules/structure of the environment, retailers’ have similar operating/inventory costs, and each entity wants to maximize their profit. In such a world, one case to observe is when similarly operated retailers may put the same product for sale during Black Friday. The average markdown a retailer offers to consumers on Black Friday is 37%, which results in a sale price of about 2/3 of the original price. Suppose, retailers are all selling a similar product, originally priced at $100, on Black Friday and have common-knowledge of the average markdown. With a pricing domain for the product is between $20 (minimum feasible pricing) and $100 (maximum feasible pricing), retailers will eliminate dominated strategies of pricing higher than $66. Consequently, a new pricing domain for the product is formed between $20 and $66. With the common-knowledge of average markdowns on Black Friday, retailers will find previous non-dominated strategies of pricing between $66 and $44 to become dominated under the new domain and eliminate them as possibilities. When no dominated strategy is realized by any retailer, such as when retailers reach the minimum financially feasible pricing for a product, this process yields; otherwise, it continues. In Graph Theory, this process is called Iterated elimination of strictly dominated strategies (IESDS). In the last iteration of this process, retailers arrive at what is called the Nash Equilibrium, which is when each entity lacks the incentive to deviate from the chosen strategy after factoring-in their opposition’s decision.
In the current world, beyond holding their pricing or providing the best (lowest) pricing, retailers have a third strategy of matching a competitor’s pricing. When IESDS is common-knowledge to retailers, then price matching allows retailers to arrive at a Nash Equilibrium faster, which increases revenue earned from the sale. Observer the following payoff matrix (figure 1.1), such that the payoff is a sale of (originally-priced $100) product to a customer, and each store has one customer:
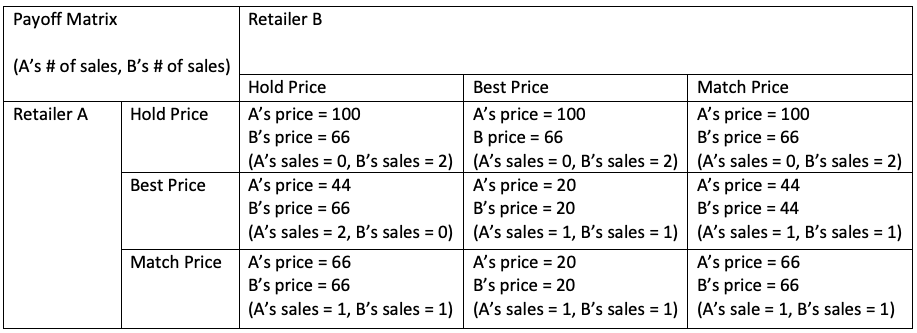
We can reason the strategy of offering the best (lowest) price yields the lowest revenue for retailers. Thus, this is a dominated strategy that should be eliminated from consideration, which forms the following payoff matrix (figure 1.2):
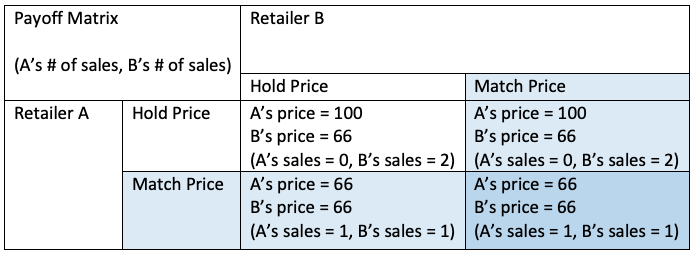
Therefore, we can understand why 21 of Canada’s largest retailers offer their customers price matching policies as it is the best non-dominated strategy.
Limitations of Game Theory on Pricing
In an imperfect world, retailers have different operating costs, varying customer loyalty, and unequal access to proprietary information via their unique big data collection about their customers. Consequently, retailers leverage customer data and buying history to provide each customer (or small groups of customers) with unique sale prices on their e-commerce website that appropriately exploits their willingness to pay. The is exemplified on e-commerce websites such as Amazon.
Sources:
https://ca.finance.yahoo.com/news/complete-black-friday-cyber-monday-130028450.html
https://ignitionframework.com/game-theory-examples-price-matching/