Sendooran Sitsabesan – CSCC46 2020 Course Blog

Using game theory and signed graphs to measure cooperation

One of the interesting concepts that we recently learned in class was game theory and payoff matrices. As we have seen in lecture, an important part of these games is that the players themselves want to maximize their payoff. In the piece, The evolution of cooperation in signed networks under the impact of structural balance, by Xiaochen He and co, they use game theory and payoff matrices to create signed network model that better helps to understand how cooperation will evolve on a graph.

First, the authors describe the PD model. The prisoner’s dilemma model using the following payoff matrix and it essentially breaks up the nodes in the graph into two separate groups: cooperators and defectors (He et al., 2018, p.4).

In these relations, the cooperators are trying to establish positive relations with other cooperators so that they can both get a payoff of R while defectors cheat cooperators and try to establish positive relations with them to get payoffs T (He et al., 2018, p.5). In doing so, this model provides an interesting abstraction towards what we have normally done with signed graphs in lecture. To my understanding, while we defined the relations of signed networks, the model used in this paper not only defines cooperative intentions in this relations, they also define strategies of how the node makes it relations by defining them as either cooperators or defectors (He et al., 2018, p.4). I thought this was an interesting model because it builds upon some of the ideas we have learned in class by adapting the payoff matrices from game theory and applying it to signed graphs.

Following this, the authors then apply structural balance onto this model and help describe how this affects what balanced triangles would look like on the graph. It goes as following

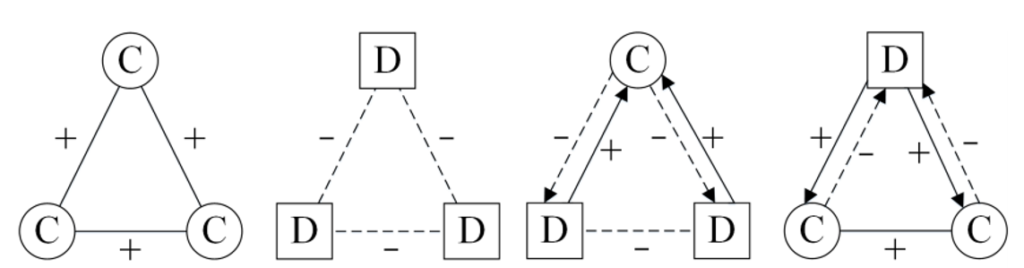
While the ideal triangles of the PD model look as such, we can clearly see that some would not fit within the definition of structural balance. By applying structural balance, the authors insist that the only possible balanced triangles would be where we had three cooperators where each had positive relations with one another, and where we had two cooperators with a positive relation whom had negative relations with the defector (He et al., 2018, p.5). This follows what we have learned in class as these triangles have either one or three positive edges.

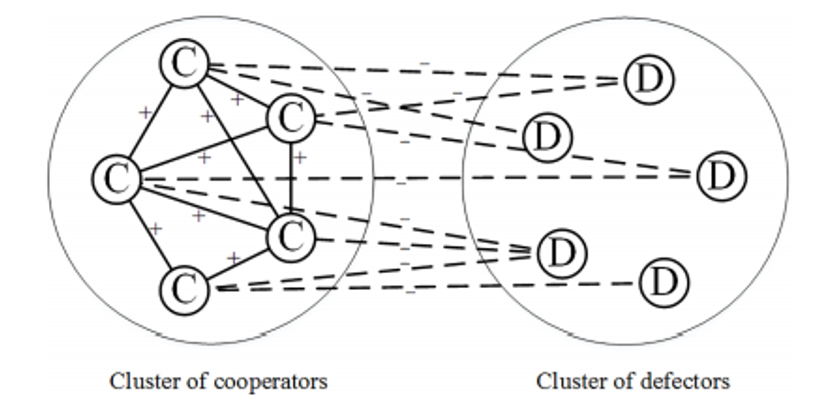
With structural balance, we have a network where we have our cluster of cooperators and their positive edges and then we have another cluster of defectors who share no edges with one another but receive negative edges from nodes within the cooperator cluster (He et al., 2018, p.5).

To test cooperation, the authors used Erdos-Renyi graphs and applied an algorithm to update their edges and behaviors iteratively (He et al., 2018, p.10). They did so under multiple different criteria, each differing in their usage of structural balance. In doing so, they could see how the usage of structural balance affects how the graph evolves over multiple iterations.

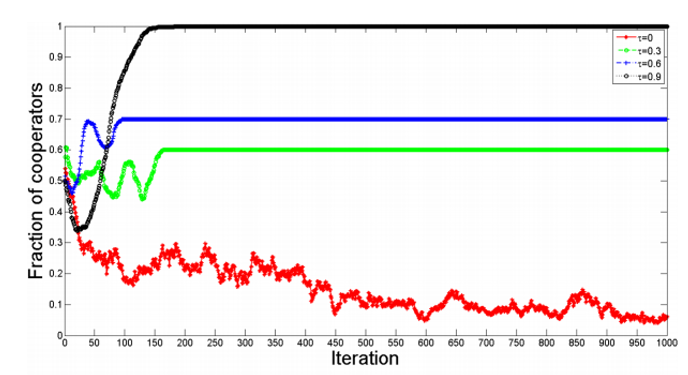
Fraction of Cooperators without structural balance

In the case of not using structural balance, they noticed that as the probability of an update of a node increased (i.e. τ approaches 1), the graph would become entirely composed of cooperators with positive edges (He et al., 2018, p.9-10).

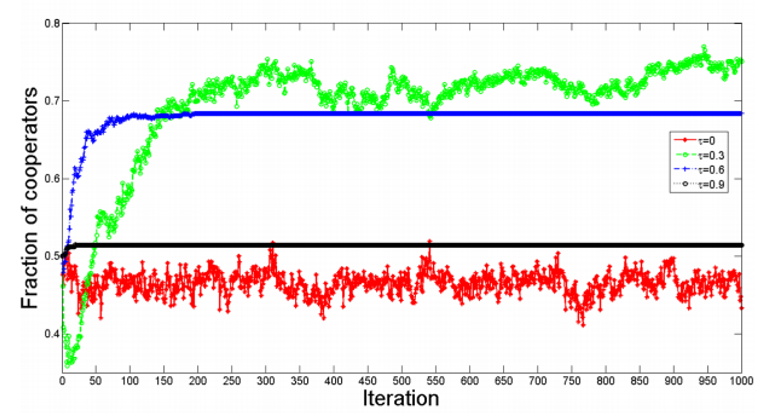
Fraction of Cooperators with structural balance

In contrary, when using structural balance, while the fraction of cooperators increases, there will still always be some defectors (He et al., 2018, p.12). As such, the authors suggest that in structural balance, it is not possible to remove the defectors because of how the balanced triangles work (He et al., 2018, p.12). For instance, it makes sense that all cooperators will have positive edges as they are share the same payoff. In the case of two cooperators with one defector, since the cooperators have negative edges towards the defector, there is no incentive for the defector to become a cooperator since it would be lessening its payoff unless it was able to cause the edges to switch signs (He et al., 2018, p.12). In doing so, we likely will be stuck with the defector and the balanced triangle.

To conclude, the authors reiterate that the implementation of structural balance in their iterative model ends up with their graph containing both cooperators and defectors with the two specific balanced triangles and that cooperation succeeds as the probability of the edges switching signs increases (He et al., 2018, p.14).

I personally found this paper interesting as it uses game theory and signed networks and creates a model that combines both concepts. Furthermore, the model is interesting in evaluating cooperation. We could use this model in different contexts that contain two different groups of individuals, one where they have incentive to cooperate and one where they have incentive to cheat others. An example could be competitive environments like schooling where there are those would cooperate and make clusters and those who would not (i.e not doing work in group projects).

References:

He, X., Du, H., Cai, M., Feldman, M.W. (2018). The evolution of cooperation in signed networks under the impact of structural balance. PLoS ONE 13(10): e0205084. https://doi.org/10.1371/journal.pone.0205084

Link: https://doaj.org/article/84f0041b0eeb46ad81c07e5d57deb093

Using graphs to evaluate sports performance

As an avid viewer of sports, I am always seeking ways to see how the concepts I learn in class could be applied in evaluating sports performance. Regarding graph theory, the authors Ribeiro, Silva and co have attempted to create a graph-based mathematical model that can better display micro and macro analysis of player performance.

In the piece, the authors first explain why graph theory can be applied to sports. As most sports are cooperative in nature and require the movement of some sort of ball, they are ripe for use in graphs. One of the key fallouts of regularly used statistics for sports that the authors bring up is that they do not properly represent spatial scales (Ribeiro et al., 2017, p.1690). For instance, while passes completed by a player in a soccer game may help in knowing how well a player can pass the ball, it does not reflect how well the player gets the ball down the pitch. A player could complete low risk passes but some may favour a player who makes less passes accurately but gets the ball into scoring position.

For the graphs themselves, the authors present two possible graph types to choose.

Two different graphs we can use to evaluate sport performance

In reference to weighted graphs, the authors mention how graph weight could be relevant in context. For instance, weight could be used as the count of passes made between players in a soccer pitch. Additionally, the authors present an application of graph theory that uses weighted graphs and their associated adjacency matrices to evaluate a soccer team’s passing performance.

An example of graph use for a passing network in soccer

In this example, the authors use nodes to display players and wider edges to demonstrate weights of how often a pass is made between two players. In doing so, the authors display how some common graph calculations could better explain player performance in this context. Degree centrality, for instance, is how many edges that include a node (Ribeiro et al., 2017, p.1694). Using this, we can see in how many passes a player is involved in. Another key value could be the betweenness centrality, which is how often a node appears in the various shortest paths between any pair of nodes (Ribeiro et al., 2017, p. 1694). This helps to show how involved a node/player is in the passing network. By using graph concepts, like node degrees, the authors are showing us the application of graphs in assessing sport performance.

Overall, while the authors demonstrate the effectiveness of graph theory in evaluating a soccer team’s passing network, they also identify some key issues with generalizing their models over different sports. First, it is not easy to use the same node and edge classifications for a sport with little to no passing (Ribeiro et al., 2017, p. 1694). An example that I immediately thought of as I read the piece was American football. Outside of laterals, the majority of passing in the sport is done by the quarterback and so using passes as edges in that graph model may not work as most edges would come from one node.

Another key issue is that their models and the other studies they referred to in their piece do not properly demonstrate the variance of player performance in different situations (Ribeiro et al., 2017, p. 1694). As an example, their models do not display player performance over time (Ribeiro et al., 2017, p. 1694). Regarding this, I think a way to incorporate time into the graphs is to break up the passes done over various periods of time. While this would result in a multitude of graphs, it does give us the opportunity to see how our pass networks differ as time progresses. In the example above with soccer, if a player’s degree centrality falls immensely over time, we would see this as the amount of edges originating from the node decreasing over time. As such, it may make sense for a coach to then substitute the player after a certain amount of time.

I personally found this piece interesting because it gives us an application of graph theory we have not seen in class and it also shows some issues with using graphs to represent other contexts. By showing us how the application of graph theory in sports, it also brings up the importance of properly defining our nodes and edges when creating a mathematical model. While their model works well with models based around passing, there is work needed to be done to properly evaluate other sports networks.

References:

Ribeiro, J., Silva, P., Duarte, R., Davids, K., & Garganta, J. (2017). Team Sports Performance Analysed Through the Lens of Social Network Theory: Implications for Research and Practice. Sports Medicine, 47(9), 1689-1696. doi:10.1007/s40279-017-0695-1

Link: https://link-springer-com.myaccess.library.utoronto.ca/article/10.1007/s40279-017-0695-1