With Black Friday around the corner, North America will have a very different experience of this retail holiday than the last decade.

Since the inception of malls, shopping in person has been wildly popular amongst consumers, they are able to view their products and try it before purchasing, which are major benefits for making the payment decision. However, competition arose when online giants such as Amazon, eBay and various dedicated websites started to gain traction. This has created the current online shopping culture, buying from the comfort of our home and delivered to our doorsteps.

The circumstances surrounding this year is worse for retail and malls. The ongoing pandemic is likely to last through most of the major holidays for shopping; Black Friday, Cyber Monday and Boxing Day. Many of the retail chains have already been closing down some of their less prominent locations and with social distancing and various lockdown throughout the current event, shopping in person has never been more unpopular. On the other hand, the boom of online shopping is going on strong as it became one of the best ways to cure our retail needs in this global situation. Not all hope is lost, with every turn of events comes an opportunity. At the moment, many of the stores are closing their physical location, this in turn opens up more avenues for bigger chains to leverage.

One of the interesting factors about Game Theory, is that it even appears in choosing the location for retail shops. The reason why similar businesses open next to each other is due to this configuration being the Pure Nash Equilibrium where both parties cannot deviate from the current location to gain anymore benefit.

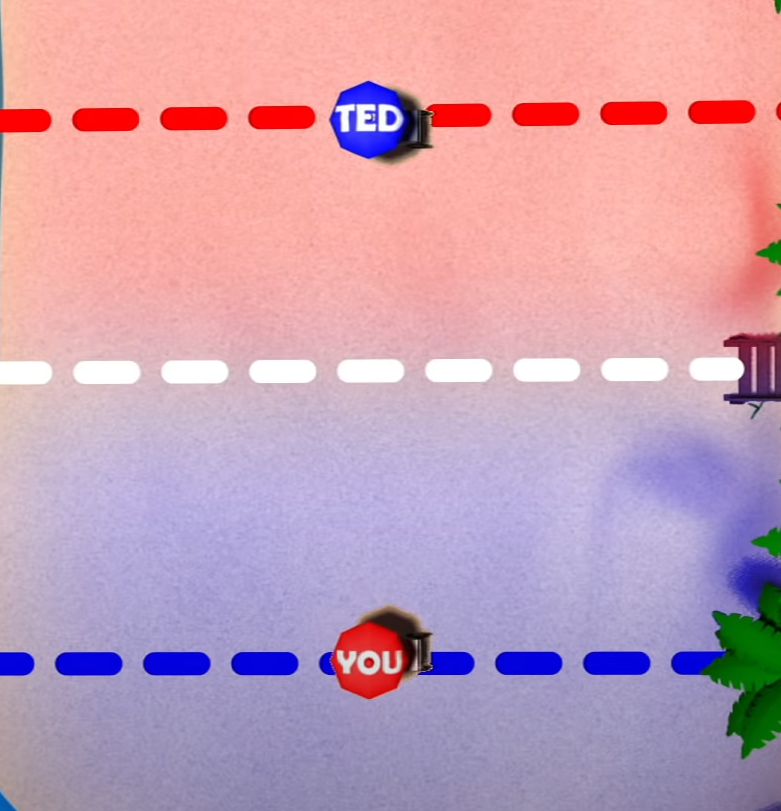
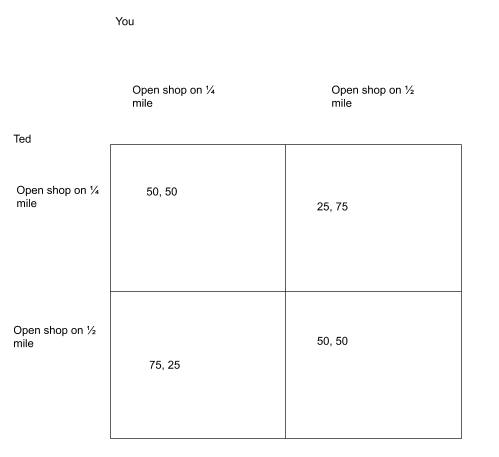
Let us consider the following situations (from TED-ED)¹. Two competitors are selling ice cream on the beach. In the first scenario where a line down the middle separates them, and they each occupy their own halves. In this case, both parts would get half of the sales, but there is a better play for one of the stores. Consider figure 2, where Ted moves to the middle, now he gets his original sale and splits the sale between ½ mile and ¼ with you. Both parties would continue to move to the advantageous position until they both settle down in the center where they cannot deviate from that position to gain any benefits.

Figure 3: both parties reaches Nash equilibrium

Figure 4: payoff matrix, we can see Pure Nash Equilibrium is opening shop at the ½ mile together.

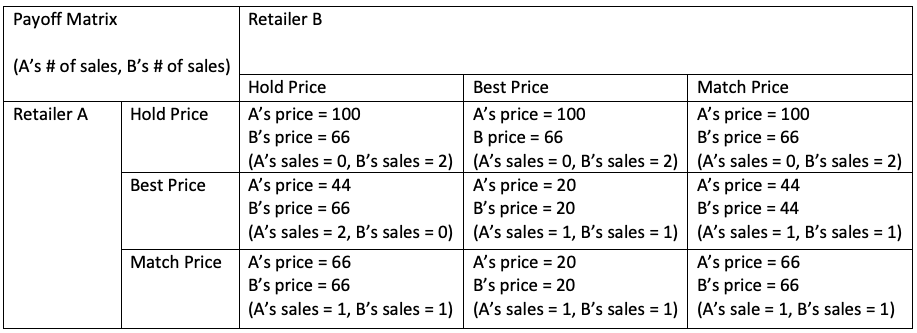
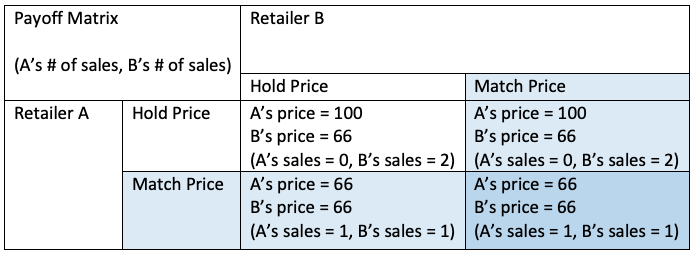
How this does apply to the current pandemic? With the closing of many stores, the bigger players of retail sector can purchase more storefronts to obtain a bigger payout than their competitors in physical locations. Consider the previous scenario, however, this time Ted has 2 stores instead. In that case, you will always obtain a lower payout than Ted where he can surround your store on either ends and taking over half your sales. Normally, this would not be achievable due to the cost of purchasing storefronts and competitors owning a location nearby. But this pandemic has opened up many retail spaces for taking.

Next, let us consider the e-commerce side of shopping. With the current pandemic, a lot of the purchases are being made online in e-commerce giants like Amazon. With this in mind, would it be more beneficial for current market to purchase more storefronts to attack competitors on the physical locations side, or is the money better spent on establishing their own online store and delivery routes instead? The answer to this question lies within the payoff of each situation and it’s hard to calculate without knowing the specific numbers. Even with the current pandemic, we can see that the percentage of sales rising from e-commerce is still only a fraction of the sales a store can gain from having a physical location. However, we are comparing the gains of purchasing more storefronts vs diversifying and investing the funds into producing an online shopping solution. If we were to construct a payoff matrix, the matrix itself would not have any Pure Nash equilibrium and instead would be mixed strategy. As the best strategy would depend on the expected payout and the company would then split their funds accordingly.

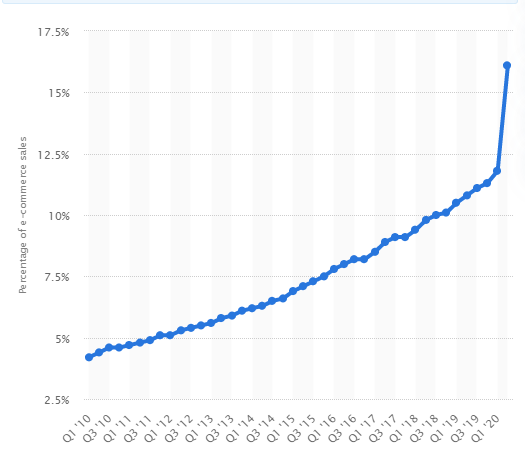
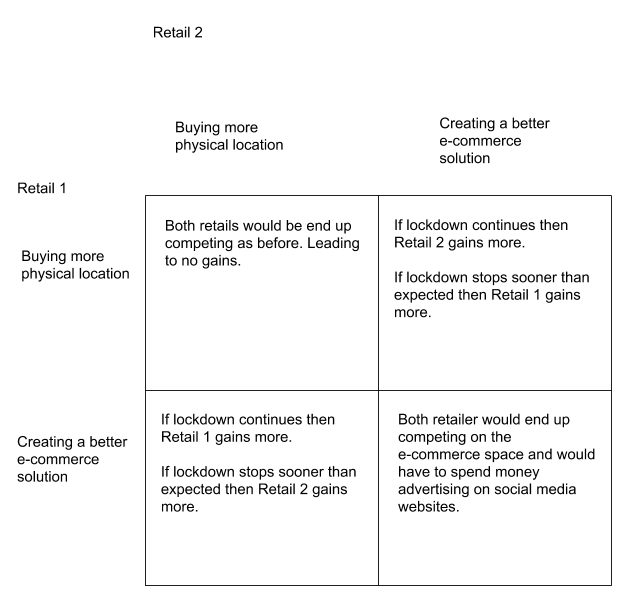
Figure 5: percentage of E-commerce sales of total retail sales (Statista)

Figure 6: Example of a payoff matrix for investing into physical location vs online solution.

In conclusion, this Black Friday might be the first mark towards a very different shopping experience in the next decade. If the sales figure points to online shopping producing a better net sale, then it is possible more retail giants would not hesitate to close down their less popular locations and invest into a better e-commerce. However, if the sales figure points towards the traditional method being superior, then we might see the bigger players of retail popping up more stores over the next few years. Although, a major factor to consider, and the creator of this situation, is how long will lockdown and the global pandemic last. This factor will also be a major player in deciding the retail landscape for the next decade.

Source

At the time of writing this post, Canada’s largest sale event, Black Friday, is about 20 days away. This week, Yahoo Finance released an article called, “Your Complete Black Friday and Cyber Monday Shopping Strategy for 2020”. During the Black Friday event, consumers will be developing optimal shopping strategies to get the best deals. Additionally, retailers are constructing strategies to market and price their product to maximize their sales over their competitors. By using the material taught regarding Game Theory in CSCC46 we can understand an optimal pricing strategy in a perfect world, and how this strategy fits in an imperfect one.

Game Theory on Black Friday Pricing

In a perfect world, we may assume all entities are rotational, all entities know the rules/structure of the environment, retailers’ have similar operating/inventory costs, and each entity wants to maximize their profit. In such a world, one case to observe is when similarly operated retailers may put the same product for sale during Black Friday. The average markdown a retailer offers to consumers on Black Friday is 37%, which results in a sale price of about 2/3 of the original price. Suppose, retailers are all selling a similar product, originally priced at $100, on Black Friday and have common-knowledge of the average markdown. With a pricing domain for the product is between $20 (minimum feasible pricing) and $100 (maximum feasible pricing), retailers will eliminate dominated strategies of pricing higher than $66. Consequently, a new pricing domain for the product is formed between $20 and $66. With the common-knowledge of average markdowns on Black Friday, retailers will find previous non-dominated strategies of pricing between $66 and $44 to become dominated under the new domain and eliminate them as possibilities. When no dominated strategy is realized by any retailer, such as when retailers reach the minimum financially feasible pricing for a product, this process yields; otherwise, it continues. In Graph Theory, this process is called Iterated elimination of strictly dominated strategies (IESDS). In the last iteration of this process, retailers arrive at what is called the Nash Equilibrium, which is when each entity lacks the incentive to deviate from the chosen strategy after factoring-in their opposition’s decision.

In the current world, beyond holding their pricing or providing the best (lowest) pricing, retailers have a third strategy of matching a competitor’s pricing. When IESDS is common-knowledge to retailers, then price matching allows retailers to arrive at a Nash Equilibrium faster, which increases revenue earned from the sale. Observer the following payoff matrix (figure 1.1), such that the payoff is a sale of (originally-priced $100) product to a customer, and each store has one customer:

We can reason the strategy of offering the best (lowest) price yields the lowest revenue for retailers. Thus, this is a dominated strategy that should be eliminated from consideration, which forms the following payoff matrix (figure 1.2):

Therefore, we can understand why 21 of Canada’s largest retailers offer their customers price matching policies as it is the best non-dominated strategy.

Limitations of Game Theory on Pricing

In an imperfect world, retailers have different operating costs, varying customer loyalty, and unequal access to proprietary information via their unique big data collection about their customers. Consequently, retailers leverage customer data and buying history to provide each customer (or small groups of customers) with unique sale prices on their e-commerce website that appropriately exploits their willingness to pay. The is exemplified on e-commerce websites such as Amazon.

Sources:

https://ca.finance.yahoo.com/news/complete-black-friday-cyber-monday-130028450.html

https://ignitionframework.com/game-theory-examples-price-matching/

https://spendmenot.com/blog/black-friday-sales-statistics/

https://www.investopedia.com/terms/n/nash-equilibrium.asp#:~:text=More%20specifically%2C%20the%20Nash%20equilibrium,after%20considering%20an%20opponent’s%20choice

https://www.howtosavemoney.ca/canadian-price-match-policies