Tag: game theory

Game theory shows the downward trend of Climate Change

Post author By Muhammad Sajidur Rahman
Post date November 20, 2020
No Comments on Game theory shows the downward trend of Climate Change

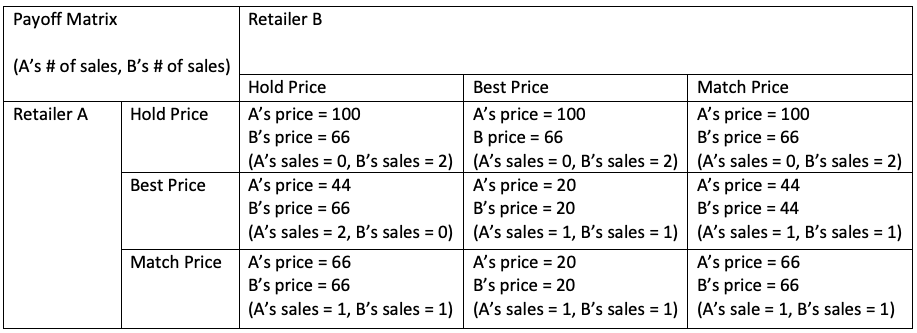
During one of our recent lectures, we were introduced to Game Theory and the modelling of simple two player games in a 2 by 2 matrix that consist of payoff values which sometimes vary depending on not just the decision the player chooses, but also depending on what the opposing player chooses too. This topic is a good way to explain the current climate change situation through various scenarios.

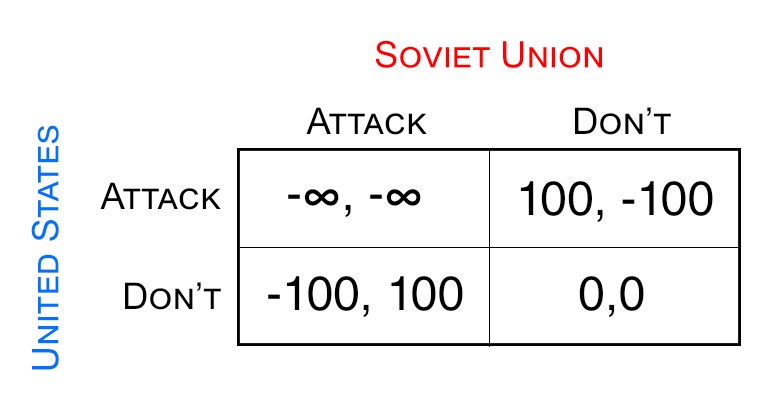
The bottom line and perhaps obvious reason why countries are slow in the reduction of carbon emissions and introducing policies to the benefit of the environment is because exploitation is profitable. At the present, from an economic perspective, using the resources we have provides the most individual benefit to its own nation. Thus even if two states or nations X and Y cooperate right now, looking at it individually there is more to gain from exploitation.

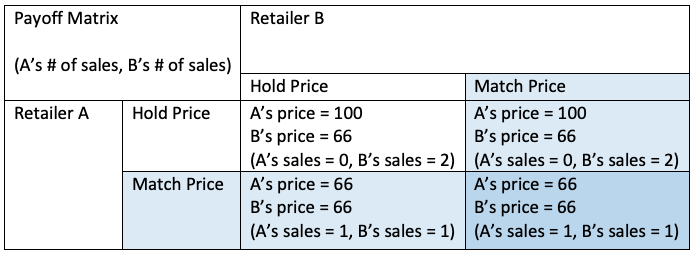
However sometime in the foreseeable future this will stop being the case. Near the collapse of our ecosystem, perhaps when we are seeing many heat storms or hurricanes or some other indicator, the priority of X and Y will now be protecting the environment. Exploitation now becomes a very unattractive option, as the need to sustain our ecosystem is critical for the survival of our planet. The other change is now that we are looking at things from the perspective of the whole ecosystem, X and Y will benefit, even if only X acts in the interest to protect the environment, since climate change is a global phenomena.

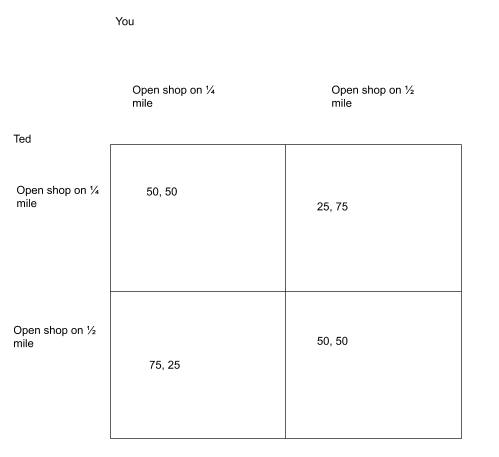
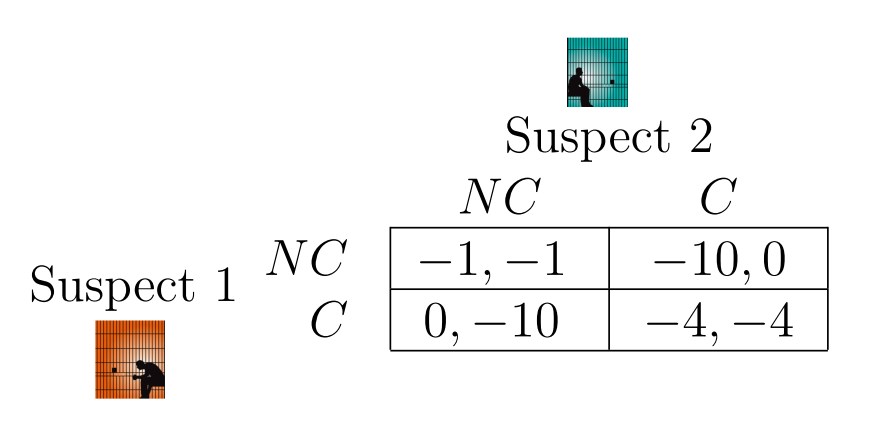
Yet, the above figure does not accurately portray both sides of the equation where there exists both the gain keeping the environment safe, but also the cost of passing environmental laws and the scenario where one nation benefits “freeloading” off of another nation enacting their policies. Let us create a scenario where the nations are the United States and China, where the situation is already at 10 point deficit. The benefit of one nation enacting policies is +3 to both nations as the environmental benefit, yet let’s say the individual nation’s cost to enact the policy is even greater at -4. We end up with a scenario like below.

T.L. is -10+3+3 for both countries since they both benefit from each other due to the environment getting better, but then go back to -4-4=-8 due to the cost of enacting their own policies.

D.L. and T.R. however have one of the nations getting the -10+3=-7 environmental benefit of the other nation without having to pay the -4 since they did not enact any policies while the other nation has a net negative with gaining their own environmental benefit but losing out due to their own cost of -10+3-4=-11

D.R. remains unchanged since neither nation enacted any policies

Thus, we can end up in a scenario where even though the best option overall looks to be the countries working together, individually it always make more sense trying to defect and not help the environment instead as the dominant strategy. This scenario mirrors the Prisoner’s Dilemma and it might be an ongoing scenario realistically between nations for many years to come before the cost of our environment will outweigh the cost for the nation to pass the environmental laws.

These are all hypothetical scenarios of course and many other factors and costs and payoffs are realistically put in to play, but it was just a simple model showcasing what may be a realistic payoff model that would continue to deter countries from trying to fight against climate change. Hopefully, nations come to some incentive to fight for climate change earlier than later and come to a solution before we are lead to the collapse of our ecosystem.

Sources:
II, V. (2020). Is Climate Change a Prisoner’s Dilemma or a Stag Hunt?. Retrieved 20 November 2020, from https://www.theatlantic.com/notes/2016/04/climate-change-game-theory-models/479340/

Highfield, R. (2020). Climate change will get a whole lot worse before it gets better, according to game theory. Retrieved 20 November 2020, from https://www.wired.co.uk/article/climate-change-prediction-game-theory-tragedy-of-commons

Tags Climate Change, game theory

Uncategorized

Prisoner’s Dilemma in the Virtual world

Post author By Kajamugesh Raneethran
Post date November 20, 2020
1 Comment on Prisoner’s Dilemma in the Virtual world

In class, the prisoner’s dilemma was brought up to get an idea of how dominant strategy works. The prisoner’s dilemma has been shown to pop up in the real world, for example in arm races between countries and the overfishing problem; it’s easy to see why even though there is an optimal solution for both parties, the net result is one where both parties do worse. However, this issue is not just isolated in reality and I realized that similar social dilemma often arises in video games, specifically in multiplayer games.

The main reasons why many people play video games is to have fun, for the competition, or a little bit of both. However, even if you enjoy playing a game for fun rather than for competition, more often than not you will find winning much more enjoyable than losing. In many games, the most fun way to play will not be the most reliable to obtain a victory. This leads players to a dilemma in which they have to decide which strategy to pick that will counter the strategy picked by the opposing team. While competitive strategy can still be just as enjoyable as non-competitive strategies, there are times in games where the best strategy does not result in a fun time.

Online multiplayer game developers have the job of having to constantly patch a game even if there are no visible bugs. This is due to the fact that a multiplayer game that stays consistent and unchanged will grow stale and slowly lose its player base. To remedy this problem, developers will add new content to the game and make small adjustments that can change the meta in small or big ways. Unfortunately, sometimes the changes in the meta of the game are big and result in a less fun meta whether or not the developer intended for this. For example, “in the early days of StarCraft, a strategy called “Zerg rushing” emerged where at the beginning of the match players would quickly build lots of cheap Zerg units to overwhelm opponents before defenses could be constructed” (Madigan 2010). Before developer patches, this was the dominant and most used strategy of the game, even if it was not fun to play as or to play against. The prisoner dilemma perfectly explains why players kept using this strategy even though it was not every enjoyable.

From the matrix above, one can see why Zerg rushing became so common. The dominant strategy for both sides is to Zerg rush and is a strategy that is strictly better than all other options, regardless of what other players do. While a game where neither player Zerg rushes would be ideal, if one player chooses not to Zerg rush, the other player will have more incentive to Zerg rush since they would have more enjoyment dominating the game than they would in a normal match. As a result, both players Zerg rush and the games are unsatisfying to play.

Another issue that comes from developers patching a game and adding new content is the inevitable bugs that come along with that content. Sometimes these bugs and glitches will be small and not usually have much impact on the game, but there are times when exploiting these bugs is a legitimate strategy that results in a more likely victory. For instance, “some players of the online first-person shooter Modern Warfare 2 discovered what became known as “the javelin glitch.” Someone, somewhere, somehow figured out that through a bizarre sequence of button presses you could glitch the game so that when you died in multiplayer you would self destruct and murder everyone within 30 feet, often resulting in a net gain in points” (Madigan 2010). Modern Warfare players end up in a similar dynamic as the Zerg rush problem where they have to decide which strategy will result in a more positive outcome.

Once again, even though not exploiting the glitch would result in fair play that is optimal for both parties, instead the more common route was mayhem where all players exploited this glitch. This was so common in fact that Infinity Ward had to rush out a patch to stop it from being exploited any further. Using the same logic as the prisoner’s dilemma we can see that the dominant strategy for all players would be to glitch. The players would rather have a broken match than be dominated by opposing players.

In conclusion, the prisoner’s dilemma and game theory allow for a better understanding of social dilemmas in not just the real world, but also the virtual world. I believe that game developers at the very least can use this information to prevent players from having to be put in future dilemmas, such as by banning players that exploit bugs so that the pay off matrix will result in a dominant strategy that is fun for all players.

Sources:

Madigan, J., Says. (2013, July 30). The Glitcher’s Dilemma: Social Dilemmas in Games. Retrieved November 18, 2020, from https://www.psychologyofgames.com/2010/03/279/

Tags cscc46, game theory

Uncategorized

Changes in Landscape for Retail and Malls

Post author By Jiale Yang
Post date November 20, 2020
No Comments on Changes in Landscape for Retail and Malls

With Black Friday around the corner, North America will have a very different experience of this retail holiday than the last decade.

Since the inception of malls, shopping in person has been wildly popular amongst consumers, they are able to view their products and try it before purchasing, which are major benefits for making the payment decision. However, competition arose when online giants such as Amazon, eBay and various dedicated websites started to gain traction. This has created the current online shopping culture, buying from the comfort of our home and delivered to our doorsteps.

The circumstances surrounding this year is worse for retail and malls. The ongoing pandemic is likely to last through most of the major holidays for shopping; Black Friday, Cyber Monday and Boxing Day. Many of the retail chains have already been closing down some of their less prominent locations and with social distancing and various lockdown throughout the current event, shopping in person has never been more unpopular. On the other hand, the boom of online shopping is going on strong as it became one of the best ways to cure our retail needs in this global situation. Not all hope is lost, with every turn of events comes an opportunity. At the moment, many of the stores are closing their physical location, this in turn opens up more avenues for bigger chains to leverage.

One of the interesting factors about Game Theory, is that it even appears in choosing the location for retail shops. The reason why similar businesses open next to each other is due to this configuration being the Pure Nash Equilibrium where both parties cannot deviate from the current location to gain anymore benefit.

Let us consider the following situations (from TED-ED)¹. Two competitors are selling ice cream on the beach. In the first scenario where a line down the middle separates them, and they each occupy their own halves. In this case, both parts would get half of the sales, but there is a better play for one of the stores. Consider figure 2, where Ted moves to the middle, now he gets his original sale and splits the sale between ½ mile and ¼ with you. Both parties would continue to move to the advantageous position until they both settle down in the center where they cannot deviate from that position to gain any benefits.

Figure 3: both parties reaches Nash equilibrium

Figure 4: payoff matrix, we can see Pure Nash Equilibrium is opening shop at the ½ mile together.

How this does apply to the current pandemic? With the closing of many stores, the bigger players of retail sector can purchase more storefronts to obtain a bigger payout than their competitors in physical locations. Consider the previous scenario, however, this time Ted has 2 stores instead. In that case, you will always obtain a lower payout than Ted where he can surround your store on either ends and taking over half your sales. Normally, this would not be achievable due to the cost of purchasing storefronts and competitors owning a location nearby. But this pandemic has opened up many retail spaces for taking.

Next, let us consider the e-commerce side of shopping. With the current pandemic, a lot of the purchases are being made online in e-commerce giants like Amazon. With this in mind, would it be more beneficial for current market to purchase more storefronts to attack competitors on the physical locations side, or is the money better spent on establishing their own online store and delivery routes instead? The answer to this question lies within the payoff of each situation and it’s hard to calculate without knowing the specific numbers. Even with the current pandemic, we can see that the percentage of sales rising from e-commerce is still only a fraction of the sales a store can gain from having a physical location. However, we are comparing the gains of purchasing more storefronts vs diversifying and investing the funds into producing an online shopping solution. If we were to construct a payoff matrix, the matrix itself would not have any Pure Nash equilibrium and instead would be mixed strategy. As the best strategy would depend on the expected payout and the company would then split their funds accordingly.

Figure 5: percentage of E-commerce sales of total retail sales (Statista)

Figure 6: Example of a payoff matrix for investing into physical location vs online solution.

In conclusion, this Black Friday might be the first mark towards a very different shopping experience in the next decade. If the sales figure points to online shopping producing a better net sale, then it is possible more retail giants would not hesitate to close down their less popular locations and invest into a better e-commerce. However, if the sales figure points towards the traditional method being superior, then we might see the bigger players of retail popping up more stores over the next few years. Although, a major factor to consider, and the creator of this situation, is how long will lockdown and the global pandemic last. This factor will also be a major player in deciding the retail landscape for the next decade.

Source

Tags Black Friday, game theory, mall, retail

Uncategorized

Explain GAN and Triple-GAN from the Perspective of Game Theory

Post author By Yifan Xu
Post date November 18, 2020
No Comments on Explain GAN and Triple-GAN from the Perspective of Game Theory

Generative adversarial network (GAN) is an exciting recent innovation in machine learning. “Given a training set, this technique learns to generate new data with the same statistics as the training set. For example, a GAN trained on photographs can generate new photographs that look at least superficially authentic to human observers, having many realistic characteristics.” (Wiki)

The algorithm of GAN can be understood as a “Minimax Zero-Sum Non-Cooperative Game” that two neural networks, generative network, and discriminative network, are contesting against each other in the game. The generative model is trained to produce authentic images to fool the discriminator, and the discriminator is trained to distinguish between fake images produced by the generative model and the real images.

Researchers found that it is difficult to train GAN as the two networks cannot reach the optimal at the same time. This phenomenon can be explained by why it is difficult to find the Nash Equilibrium using gradient descent.

Consider a Minimax game with two players A and B, which control the value of x and y, respectively. Player A wants to maximize the value xy while B wants to minimize it. Analytically, we know that the equilibrium reaches when x=0 or y=0.

However, if we update the parameter x and y based on the gradient of the value function V, from figure 5, we find x and y are oscillating around 0 and do not converge. Hence, gradient descent has flaws to find the Nash equilibrium.

Researchers have also found it is often the case that the discriminator can reach near-optimal, and the generator is unable to model the distribution of the true data. Triple-GAN was proposed to improve the performance of the generator by introducing a third player, classifier. The utilities of the generator and discriminator differ from the ones in GAN slightly. The generator and the classifier characterize the conditional distributions between images and labels, and the discriminator solely focuses on identifying fake image-label pairs. The authors of the paper proved that when the class conditional distribution between the classifier and the generator becomes close, the generator and classifier can nearly model the true data distribution. Hence, Triple-GAN introduces a term R_L that penalizes the loss function if the class conditional distribution between the classifier and the generator diverges too much.

Now, take a look at how Triple-GAN has reshaped the dynamics of the game. The generator and classifier are trained to fool the discriminator, and the discriminator is trained to distinguish fake image-label pairs. But this time, the cooperative characteristic is introduced to the game. As mentioned in the paragraph above, the loss function is penalized if the class conditional distribution between classifier and generator diverges too much. In other words, the classifier and generator lose points if they have the same class distribution. And thanks to the cooperation with the classifier , the generator is able to choose a better strategy for itself and can model the true distribution data more closely.

References:

1: https://arxiv.org/pdf/1703.02291.pdf

2:https://arxiv.org/pdf/1406.2661.pdf

3:https://jonathan-hui.medium.com/gan-why-it-is-so-hard-to-train-generative-advisory-networks-819a86b3750b

4:https://en.wikipedia.org/wiki/Generative_adversarial_network

Tags game theory, GAN, Machine Learning, Nash Equilibrium

Uncategorized

Game Theory in Nuclear War Strategy

Post author By Abhay Vaidya
Post date November 15, 2020
No Comments on Game Theory in Nuclear War Strategy

When discussing game theory, it’s easy to forget its applications beyond just games, as the name would deceptively suggest. The mathematical field of game theory can provide elegant ways to strategize very real and difficult problems. When I was reading the blog post titled ‘Coordination Failure’ by Linda, I found the mention of the nuclear arms race most fascinating. This was also briefly brought up in the blog post titled ‘Balance of Top Countries, A View of Their Relationship Network’ by Jiale. This prompted me to do more research and further uncover how game theory can be applied to arguably one of the most serious and/or dangerous situations we face as a society.

I came across an analytical article from The Washington Post called ‘What game theory tells us about nuclear war with North Korea’ by Elizabeth Winkler. This article was written in August of 2017, when tensions between the United States and North Korea were seemingly at all time highs, with a looming threat of nuclear war. Something interesting that was pointed out in the article is that the use of game theory for military strategizing is not a new concept. In fact, it seems like we’ve done it ever since the theory itself was formalized! We’ve seen in class that what may be independently best for the players, which is what game theory aims to model, may not always be the best choice overall, which is personally a little scary considering that’s the difference between nuclear fallout and not in this case.

The article, which is actually framed as an interview between Winkler and Stanford professor Tim Roughgarden, draws parallels between nuclear strategy and the Prisoner’s Dilemma that we’ve also seen in class.

Prisoner’s Dilemma payoff matrix (Anderson, 2020)

In the Prisoner’s dilemma, the two “players” are suspects in custody who either have the option of confessing to a crime or not. Their payoff (or punishment rather) is not only dependent on what they choose to do, but also what the other suspect chooses to do. Roughgarden claims this is analogous to the United States and the Soviet Union during the Cold War. In that scenario, the (simplified) options were to either attack with nuclear weapons or not for both countries. A similar payoff matrix could be determined for the Cold War using arbitrary payoff for winning or losing:

Cold War payoff matrix using arbitrary payoff of 100/-100

There are a few differences between the Cold War era and the North Korean era. First of all, during the Cold War era, both the US and Soviet Union were neck-and-neck in terms of their capabilities to wage war. This meant that the “game” was balanced in which both players had roughly equal actions. From a game theory standpoint, this is ideal. However, naïve analyses like this are flawed in that they don’t take into account repeated games. For example, it’s likely in a country’s best interest to attack, but this can cause other parties to behave differently in the future. The article mentions that the conflict between US and North Korea is almost a second round or repeated “game” of the US and Soviet Union one.

When asked what action the US should take, Roughgarden refers to an example that we’ve seen in class where two people would prefer to go to dinner together, but have different food preferences. This idea of multiple Nash equilibria where there are multiple best options isn’t clear from the payoff matrix above, but that’s because of another flaw of applying game theory to analyze war strategy. Roughgarden says that it’s simply not clear what the other side will do or how rational they may behave. We know from class that the models we have learned require the assumption of equally rational parties. But people are people and it’s never as simple as that. Personally, this gets me more excited than ever to learn about how more advanced game theories account for unbalanced players with better accuracy.

References

Winkler, Elizabeth. “Analysis | What Game Theory Tells Us about Nuclear War with North Korea.” The Washington Post, WP Company, 29 Apr. 2019, www.washingtonpost.com/news/wonk/wp/2017/08/16/what-game-theory-tells-us-about-nuclear-war-with-north-korea/.

Linda. “Coordination Failure.” CSCC46 2020 Course Blog, 13 Nov. 2020, cmsweb.utsc.utoronto.ca/c46blog-f20/2020/11/13/coordination-failure/.

Yang, Jiale. “Balance of Top Countries, A View of Their Relationship Network.” CSCC46 2020 Course Blog, 23 Oct. 2020, cmsweb.utsc.utoronto.ca/c46blog-f20/2020/10/23/balance-of-top-countries-a-view-of-their-relationship-network/.

Anderson, Ashton. “Lecture 8.” Social and Information Networks. www.cs.toronto.edu/~ashton/cscc46/lectures/lecture8-2020.pdf.

Tags game theory, Nuclear War

Uncategorized

Gaming Black Friday

At the time of writing this post, Canada’s largest sale event, Black Friday, is about 20 days away. This week, Yahoo Finance released an article called, “Your Complete Black Friday and Cyber Monday Shopping Strategy for 2020”. During the Black Friday event, consumers will be developing optimal shopping strategies to get the best deals. Additionally, retailers are constructing strategies to market and price their product to maximize their sales over their competitors. By using the material taught regarding Game Theory in CSCC46 we can understand an optimal pricing strategy in a perfect world, and how this strategy fits in an imperfect one.

Game Theory on Black Friday Pricing

In a perfect world, we may assume all entities are rotational, all entities know the rules/structure of the environment, retailers’ have similar operating/inventory costs, and each entity wants to maximize their profit. In such a world, one case to observe is when similarly operated retailers may put the same product for sale during Black Friday. The average markdown a retailer offers to consumers on Black Friday is 37%, which results in a sale price of about 2/3 of the original price. Suppose, retailers are all selling a similar product, originally priced at $100, on Black Friday and have common-knowledge of the average markdown. With a pricing domain for the product is between $20 (minimum feasible pricing) and $100 (maximum feasible pricing), retailers will eliminate dominated strategies of pricing higher than $66. Consequently, a new pricing domain for the product is formed between $20 and $66. With the common-knowledge of average markdowns on Black Friday, retailers will find previous non-dominated strategies of pricing between $66 and $44 to become dominated under the new domain and eliminate them as possibilities. When no dominated strategy is realized by any retailer, such as when retailers reach the minimum financially feasible pricing for a product, this process yields; otherwise, it continues. In Graph Theory, this process is called Iterated elimination of strictly dominated strategies (IESDS). In the last iteration of this process, retailers arrive at what is called the Nash Equilibrium, which is when each entity lacks the incentive to deviate from the chosen strategy after factoring-in their opposition’s decision.

In the current world, beyond holding their pricing or providing the best (lowest) pricing, retailers have a third strategy of matching a competitor’s pricing. When IESDS is common-knowledge to retailers, then price matching allows retailers to arrive at a Nash Equilibrium faster, which increases revenue earned from the sale. Observer the following payoff matrix (figure 1.1), such that the payoff is a sale of (originally-priced $100) product to a customer, and each store has one customer:

We can reason the strategy of offering the best (lowest) price yields the lowest revenue for retailers. Thus, this is a dominated strategy that should be eliminated from consideration, which forms the following payoff matrix (figure 1.2):

Therefore, we can understand why 21 of Canada’s largest retailers offer their customers price matching policies as it is the best non-dominated strategy.

Limitations of Game Theory on Pricing

In an imperfect world, retailers have different operating costs, varying customer loyalty, and unequal access to proprietary information via their unique big data collection about their customers. Consequently, retailers leverage customer data and buying history to provide each customer (or small groups of customers) with unique sale prices on their e-commerce website that appropriately exploits their willingness to pay. The is exemplified on e-commerce websites such as Amazon.

Sources:

https://ca.finance.yahoo.com/news/complete-black-friday-cyber-monday-130028450.html

https://ignitionframework.com/game-theory-examples-price-matching/

https://spendmenot.com/blog/black-friday-sales-statistics/

https://www.investopedia.com/terms/n/nash-equilibrium.asp#:~:text=More%20specifically%2C%20the%20Nash%20equilibrium,after%20considering%20an%20opponent’s%20choice

https://www.howtosavemoney.ca/canadian-price-match-policies